动态规划

动态规划

一般类型

70. 爬楼梯（Easy）

先分析一下三个台阶时的情况：

  • 从台阶 1 跨两步到 3
  • 从台阶 2 跨一步到 3

所以如果我们用数组 dp 存储每个台阶数对应的爬法，那么 dp[i] = dp[i-1] + dp[i-2] 。这样我们就得到了递推（状态转移）公式了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int climbStairs(int n)
{
    if (n == 1) return 1;
	
    // 存储不同台阶数对应的爬法的 dp 数组
    vector<int> dp(n+1);
    // 初始化 dp，n = 0 没有意义
    dp[1] = 1; dp[2] = 2;

    for (int i = 3; i <= n; i++)
        dp[i] = dp[i-1] + dp[i-2];

    return dp[n];
}

但是实际上，从递推公式可以知道，当前的状态只与前两个状态有关，所以可以只用大小为 2 的数组来保存前两个状态

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int climbStairs(int n)
{
    if (n == 1) return 1;

    int dp[2] = {1, 2};

    for (int i = 3; i <= n; i++)
    {
        int sum = dp[0] + dp[1];
        dp[0] = dp[1];
        dp[1] = sum;
    }

    return dp[1];
}

746. 使用最小花费爬楼梯（Easy）

首先明确 dp 存储爬到对应楼梯需要的花费。这样可以确定：

  • dp[i] = dp[i-1] + cost[i-1]
  • dp[i] = dp[i-2] + cost[i-2]

此外，第 0 和 1 个台阶不需要花费，所以

  • dp[0] = 0
  • dp[1] = 0

这样我们可以确定递推公式：dp[i] = min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2])

1
2
3
4
5
6
7
8
9
10
int minCostClimbingStairs(vector<int>& cost)
{
    vector<int> dp(cost.size()+1);
    dp[0] = dp[1] = 0;

    for (int i = 2; i <= cost.size(); i++)
    	dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]);

    return dp[cost.size()];
}

同样的，因为每层台阶只与前两层相关，所以可以用大小为2的数组来记录

1
2
3
4
5
6
7
8
9
10
11
12
13
int minCostClimbingStairs(vector<int>& cost)
{
    int dp[2] = {0, 0};

    for (int i = 2; i <= cost.size(); i++)
    {
        int tmp = min(dp[0]+cost[i-2], dp[1]+cost[i-1]);
        dp[0] = dp[1];
        dp[1] = tmp;
    }

    return dp[1];
}

62. 不同路径（Medium）

用深度搜索是可以解决这个问题的，但是会超时。而且本体不需要记录路径，所以使用 dp 更合适。

分析可知，从左上角出发，到达网格中任意的格的走法，都与该格的上和左格的走法相关：

  • dp[i] = dp[i-1][j] + dp[i][j-1]

特殊情况是，第一行和第一列所有格子都只有一种走法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int uniquePaths(int m, int n)
{
    vector<vector<int>> dp(m, vector<int>(n, 0));
	
    // 初始化第一行和第一列
    for (int i = 0; i < n; i++) dp[0][i] = 1;
    for (int i = 0; i < m; i++) dp[i][0] = 1;
    
    for (int i = 1; i < m; i++)
    {
        for (int j = 1; j < n; j++)
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
    }

    return dp[m-1][n-1];
}

当然也可以不初始化，直接在循环中分类讨论

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int uniquePaths(int m, int n)
{
    vector<vector<int>> dp(m, vector<int>(n, 0));

    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
        {
            
            if (i > 0 && j > 0)
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            else
                dp[i][j] = 1;	// i j 中至少有一个是 0，则说明是第一行或者第一列
        }
    }

    return dp[m-1][n-1];
}

63. 不同路径 II（Medium）

该题在 62 的基础上更进一步，添加了障碍物。但实际上两者整体框架大致相同的。

对于有障碍物的格子，其走法自然是 0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid)
{
    int m = obstacleGrid.size();
    int n = obstacleGrid[0].size();
	
    // 起点或者终点有障碍，自然没有走法，直接返回
    if (obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1)
        return 0;
    
    vector<vector<int>> dp(m, vector<int>(n, 0));
    	
    // 初始化行列，遇到障碍自然后面的格子都为 0
    for (int i = 0; i < n && obstacleGrid[0][i] != 1; i++) dp[0][i] = 1;
    for (int i = 0; i < m && obstacleGrid[i][0] != 1; i++) dp[i][0] = 1;
    
    for (int i = 1; i < m; i++)
    {
        for (int j = 1; j < n; j++)
        {
            if (obstacleGrid[i][j] == 1)
                dp[i][j] = 0;
            else
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }

    return dp[m-1][n-1];
}

当然也可以不初始化，放在循环分类讨论

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid)
{
    int m = obstacleGrid.size();
    int n = obstacleGrid[0].size();

    if (obstacleGrid[0][0] == 1 || obstacleGrid[m-1][n-1] == 1)
        return 0;
	
    // 这里初始化为 1 是因为 dp[0][0] = 1
    vector<vector<int>> dp(m, vector<int>(n, 1));

    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (obstacleGrid[i][j] == 1)
                dp[i][j] = 0;
            else if (i > 0 && j > 0)
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            else if (i > 0)
                dp[i][j] = dp[i-1][j];
            else if (j > 0)
                dp[i][j] = dp[i][j-1];
        }
    }

    return dp[m-1][n-1];
}

343. 整数拆分（Medium）

该题规律较难分析。可以从列举开始分析

拆分 相乘
[2] = 1 + 1 1 x 1 = 1
[3] = 1 + 2 1 x 2 = 2
[4] = 2 + 2 2 x 2 = 4
[5] = 2 + 3 2 x 3 = 6
[6] = 3 + 3 3 x 3 = 9
[7] = 2 + 2 + 3 = 4 + 3 2 x 2 x 3 = [4] x 3
[8] = 3 + 3 + 2 = 6 + 2 3 x 3 x 2 = [6] x 2
[9] = 3 + 3 + 3 = 6 + 3 3 x 3 x 3 = [6] x 3
[10] = 3 + 3 + 4 = 6 + 4 3 x 3 x 4 = [6] x 4

可以看出，7 到 10 的部分分割在 2 到 6 中已经出现过了。似乎可以得到递推公式

  • dp[i] = j * dp[i-j] ，\(j\in [1, \frac{i}{2}]\)

为了找到最大的值，可以遍历 j

  • dp[i] = max(dp[i], j * dp[i-j])

但是这样还不能满足 2 到 6 的情况。很容易找到反例

  • dp[5] = 2 x 3 = 6 不等于 dp[2] x 3 = 2 和 dp[3] x 2 = 4

所以还需要将直接拆分成两个数相乘考虑进循环， 最后得到 递推公式：dp[i] = max(dp[i], max(i * j, j * dp[i-j]))

1
2
3
4
5
6
7
8
9
10
11
12
int integerBreak(int n)
{
    vector<int> dp(n+1, 0);
    dp[2] = 1;
    for (int i = 3; i <= n; i++)
    {
        for (int j = 1; j <= (i >> 1); j++)
            dp[i] = max(dp[i], max(j * dp[i-j], (i-j)*j));
    }

    return dp[n];
}

96. 不同的二叉搜索树（Medium）

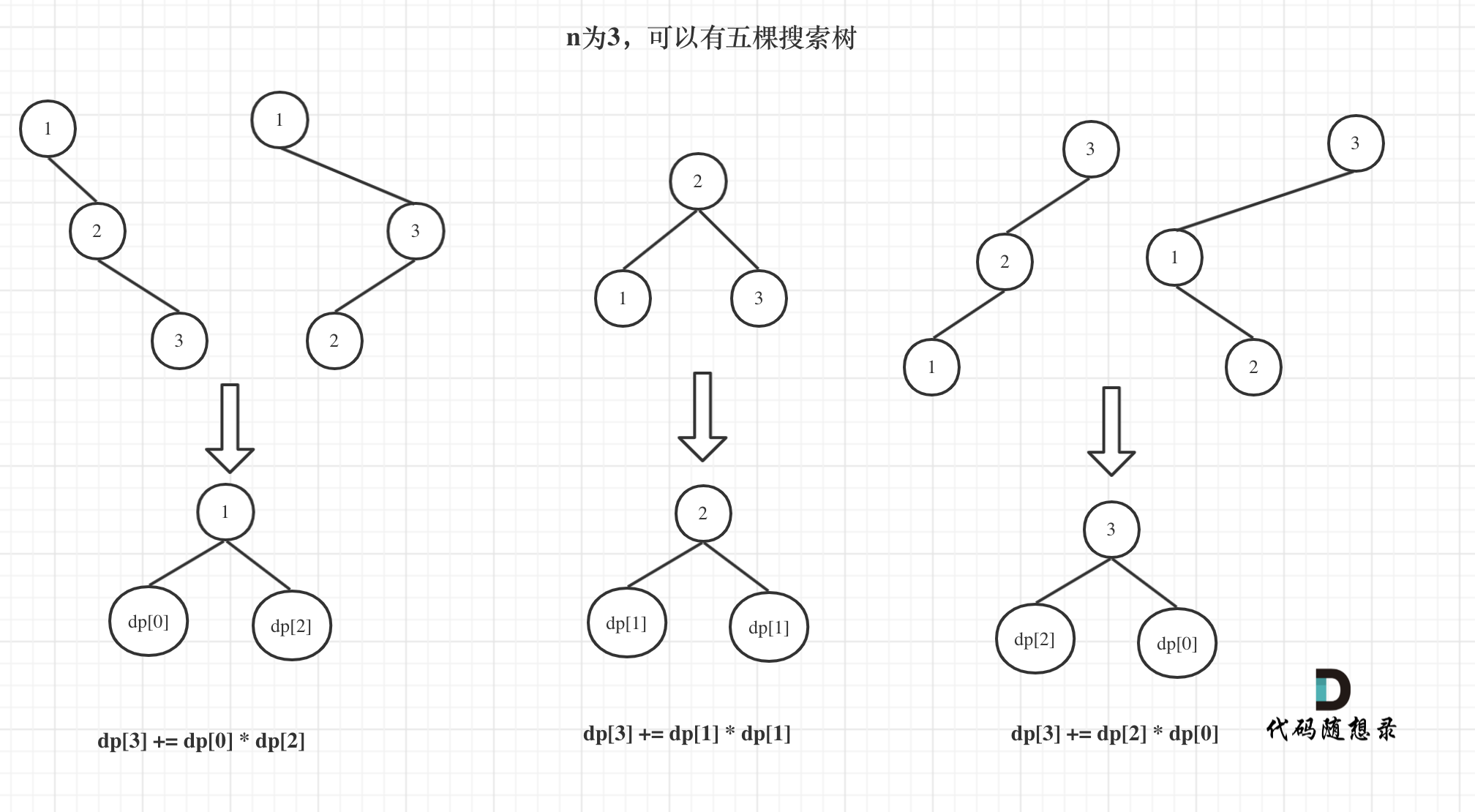
如上图所示， n 为 3 的 BST 可以分为三种情况：根为 1 ，2 ，3。这三总情况也可以继续划分子情况。

  • 根为 1，剩余两个数都大于一所以有
    • 左子树结点为 0，右子树结点为 2
  • 根为 2
    • 左子树 1，右子树 1
  • 根为 3
    • 左子树 2，右子树 0

而左右子树种类数可以根据之前的 dp 记录的到。最后可以得到递推公式

  • dp[n] = dp[0] * dp[n-1-0] + dp[1] * dp[n-1-1] + ... + dp[n-1-1] * dp[0]
1
2
3
4
5
6
7
8
9
10
11
12
13
int numTrees(int n)
{
    vector<int> dp(n+1, 0);
    dp[0] = 1; dp[1] = 1;

    for (int i = 2; i <= n; i++)
    {
        for (int j = 0; j < i; j++)
            dp[i] += dp[j] * dp[i-1-j];
    }

    return dp[n];
}

198. 打家劫舍（Medium）

比较容易想的 DP 题。数组定义如下：

  • dp[i] 表示打劫到第 i 个房子所能得到的最大金额
  • 因为不能同时打劫两个相邻的房子，所以 dp[i] 与 dp[i-1] 和 dp[i-2] 相关
    • dp[i] = max(dp[i-1], dp[i-2] + num)
      • dp[i-1] 表示当前房子不打劫
      • dp[i-2] + num 表示打劫当前房子
1
2
3
4
5
6
7
8
9
10
11
12
13
int rob(vector<int>& nums)
{
    vector<int> dp(nums.size()+1);
    dp[0] = 0; dp[1] = nums[0];
	
    // 因为有 dp[0] 所以 dp[i+1] 才是打劫到对应房子的最大金额
    for (int i = 1; i < nums.size(); i++)
    {
        dp[i+1] = max(dp[i], dp[i-1] + nums[i]);
    }

    return dp.back();
}

当然，因为只与前两个 dp 相关，所以可以压缩数组的大小

1
2
3
4
5
6
7
8
9
10
11
12
13
int rob(vector<int>& nums)
{
    vector<int> dp(2);
    dp[0] = 0; dp[1] = nums[0];

    for (int i = 1; i < nums.size(); i++)
    {
        int tmp = max(dp[1], dp[0] + nums[i]);
        dp[0] = dp[1]; dp[1] = tmp;
    }

    return dp.back();
}

213. 打家劫舍 II（Medium）

因为第一个房子和最后一个房子相邻，两者不能同时选择。

为此我们可以分开讨论

  • 第一个房子到倒数第二个房子；
  • 第二个房子到最后一个房子；

然后对两种情况取最大值即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// [bg, ed)，与 198. 打家劫舍 差别不大
int robFromTo(vector<int>& nums, int bg, int ed)
{
    vector<int> dp(2);

    dp[0] = 0; dp[1] = nums[bg];
    for (int i = bg + 1; i < ed; i++)
    {
        int tmp = max(dp[1], dp[0] + nums[i]);
        dp[0] = dp[1]; dp[1] = tmp;
    }

    return dp[1];
}

int rob(vector<int>& nums)
{
    if (nums.size() == 1) return nums[0];

    int res1 = robFromTo(nums, 0, nums.size()-1);
    int res2 = robFromTo(nums, 1, nums.size());

    return max(res1, res2);
}

337. 打家劫舍 III（Medium）

因为该题是树，通过子结点确定当前结点的最大金额可以最大程度利用树的特性。所以需要使用 后序遍历（左右中）。

每个节点向父节点返回一个二维数组，其中存储跳过子结点和选择子结点的最大金额。这样父节点可以根据这两个状态推出选中或者跳过所对应的最大金额。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 函数返回两个值
// [0] 表示跳过子节点的金额
// [1] 表示选中子节点的金额
vector<int> traversal(TreeNode* cur)
{
    // 空节点自然两个值都为 0
    if (!cur) return {0, 0};

    vector<int> left = traversal(cur->left);
    vector<int> right = traversal(cur->right);
	
    // 如果要选当前结点，则必须选 child.skipcur 即 [0]
    int selectCur = left[0] + right[0] + cur->val;
    // 不选当前结点，子结点的选与不选就要按照比较，取最大的
    int skipCur = max(left[0], left[1]) + max(right[0], right[1]);

    return {skipCur, selectCur};
}

int rob(TreeNode* root)
{
    vector<int> res = traversal(root);
    return max(res[0], res[1]);
}

0-1 背包问题

416. 分割等和子集（Medium）

该题是选子集，所以每个元素只能选一次，是 0-1 背包问题。接下来就是确定每个元素的价值，重量，和背包大小在这道题中是如何对应的。

  • 需要找到两个元素和相等的子集，实际上就是从中选取元素，如果能找到元素和为 sum / 2 的组合，则说明能够分割。
    • 确定 dp 的存储当前背包中元素的和，元素的价值就是元素本身的值。
  • 要找到元素和为总值一半的组合，其最大上限也是 sum / 2
    • 背包的大小就是 sum / 2
    • 元素自身的值也是元素的重量

现在就可以得到递推公式：dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]] + nums[i])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
bool canPartition(vector<int>& nums)
{
    int sum = 0;
    for (int& val: nums) sum += val;
    if (sum % 2 != 0) return false;		// 不能平分，说明无解

    int m = (sum >> 1);
    vector<vector<int>> dp(nums.size(), vector<int>(m+1, 0));
	
    // 初始化第0行
    // 重量为 nums[0] 及以上大小的背包都能装入 nums[0]
    for (int i = nums[0]; i <= m; i++) dp[0][i] = nums[0];

    for (int i = 1; i < nums.size(); i++)
    {
        for (int j = 0; j <= m; j++)
        {
            // 背包总大小都装不下当前值
            if (nums[i] > j) dp[i][j] = dp[i-1][j];
            else
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]] + nums[i]); // 状态转移
			
            // 找到了当前值为目标值则直接返回 true
            // 能提前返回是因为物品重量和价值相等，价值有目标值的重量自然也是目标值
            if (dp[i][j] == m) return true;
        }
    }

    return false;
}

因为状态转移公式只与上一行相关，所以可以使用滚动数组来压缩空间，减小空间复杂度。

设新的 dp[j] 存储的上一行的背包大小为 i 的总和。那么下一行可以直接在其基础上修改。得到 dp[j] = max(dp[j], dp[j-nums[i]] + nums[i])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
bool canPartition(vector<int>& nums)
{
    int sum = 0;
    for (int& val: nums) sum += val;
    if (sum % 2 != 0) return false;

    int m = (sum >> 1);
    // 第 0 行的上一行没有任何元素，自然每个背包中的总和都为 0
    vector<int> dp(m+1, 0);

    for (int num : nums)
    {
        // 因为当前的 dp[j] 与上行 dp[j] 和 dp[j-num] 相关，所以必须倒序赋值
        for (int j = m; j >= num; j--)
        {
            dp[j] = max(dp[j], dp[j-num] + num);
            if (dp[j] == m)
                return true;
        }
    }

    return false;
}

1049. 最后一块石头的重量 II（Medium）

问题的本质是，将所有石头尽量分成总重量相同的两堆。那么，这两堆的重量之差就是剩下最后一块石头的重量。

数学证明

容易理解的解释

这样，该问题就变成了类似 416. 分割等和子集 的问题。

  • 相同之处：背包大小都是 sum / 2
  • 不同和之处：该题不用一定找到大小为 sum / 2 的组合，而是尽量装满背包
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int lastStoneWeightII(vector<int>& stones)
{
    int sum = accumulate(stones.begin(), stones.end(), 0);
    int target = sum >> 1;
    vector<int> dp(target + 1, 0);

    for (int stone : stones)
    {
        for (int j = target; j >= stone; j--)
            dp[j] = max(dp[j], dp[j-stone] + stone);
    }

    return sum - dp[target] * 2;
}

494.目标和（Medium）

该题最容易想出的解法是回溯，加减分别为每层的分支，最后找到 sum == target 则说明找到一个解。但是其时间复杂度为 \(O(2^n)\)

该题因为并不需要列出解法，所以可以考虑使用 DP，不过需要对问题进一步抽象分析。

  • 该问题理解为，带负号的组合和带正号的组合之差为 target 则算一个解，数学表示为
    1. \(\sum positive-\sum negative=target\)，此外
    2. \(\sum positive + \sum negative=sum\)
    3. 1, 2可以解出 \(\sum positive = (sum + target)/2\)

所以最后问题就变为了，求总和为 (sum+target)/2 子集的数量。

那么可以确定背包的总大小为 (sum+target)/2 ，dp[i][j] 表示 装满 大小为 j 的背包时，放入0 到第 i 个元素的有多少种组合。

所以当前的 dp[i][j] 是 不放入当前元素 dp[i-1][j] 和放入当前元素 dp[i-1][j-num] 后组合数之和。

这样可以得到状态转移公式：dp[i] = dp[i] + dp[i-num]

nums = {1,1,1,1,1} 0 1 2 3 4
nums[0] 1 1 0 0 0
nums[1] 1 2 1 0 0
nums[2] 1 3 3 1 0
nums[3] 1 4 6 4 1
nums[4] 1 5 10 10 5

解释：

  • 背包大小为 0 时，不需要任何元素就已经装满背包了，所以组合为 1，dp[0][0] 到 dp[4][0] 都是 1
  • 背包大小为 1 时，加入nums[0] 能够装满，所以 dp[0][1]=1 ，而大小为 2 时无法装满，所以 dp[0][2]=0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int findTargetSumWays(vector<int>& nums, int target)
{
    int sum = accumulate(nums.begin(), nums.end(), 0);
	
    // 总和都小于目标值或者，无法得到一个整数的背包大小则一定无解
    if (target > sum || (target + sum) % 2 == 1)
        return 0;

    int bagSize = (target + sum) >> 1;
    vector<int> dp(bagSize + 1, 0);
    dp[0] = 1;
    for (int& num: nums)
    {
        for (int i = bagSize; i >= num; i--)
            dp[i] += dp[i-num];
    }

    return dp[bagSize];
}

474. 一和零（Medium）

多维背包

物品就是每个字符串，物品的价值都为 1。

背包实际上有两个大小：

  • 0 的数量 m
  • 1 的数量 n

与之对应，每个字符串的重量也是有两个：cnt0，cnt1。

因此 dp 数组应该从原来的一维（滚动数组）为二维。其递推公式为：dp[i][j] = max(dp[i][j], dp[i-cnt0][i-cnt1] + 1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int findMaxForm(vector<string>& strs, int m, int n)
{
    vector<vector<int>> dp(m+1, vector<int>(n+1, 0));

    for (string& str: strs)
    {
        int cnt0 = 0, cnt1 = 0;
        for (char& c: str) c == '0' ? cnt0++ : cnt1++;

        for (int i = m; i >= cnt0; i--)
        {
            for (int j = n; j >= cnt1; j--)
                dp[i][j] = max(dp[i][j], dp[i-cnt0][j-cnt1] + 1);
        }
    }

    return dp[m][n];
}

完全背包问题

518. 零钱兑换 II（Medium）

因为不限每个面额硬币的数量，所以该问题为完全背包问题，可以分析出：

  • 背包大小：总金额
  • 物品：硬币
    • 重量：硬币面额
  • dp[i]：代表凑出当前总金额的组合数
    • dp[0] = 1：总金额的为 0 的组合数为 1（可以理解为空集，也可以说是为了计算之后的 dp，必须为 1）

因为是求组合，所以必须让第一层循环遍历物品，第二层循环遍历背包。

1
2
3
4
5
6
7
8
9
10
11
12
int change(int amount, vector<int>& coins)
{
    vector<int> dp(amount+1, 0);
    dp[0] = 1;
    for (int& coin: coins)
    {
        for (int i = coin; i <= amount; i++)
            dp[i] += dp[i-coin];
    }

    return dp[amount];
}

377. 组合总和 Ⅳ（Medium）

本题题目描述是组合，但是从示例可以看出，实际上是排列问题。

  • 背包大小：目标值
  • 物品：数组中的数
    • 重量：每个数的数值
  • dp[i]：代表合为目标值的排列数

因为是求排列，所以必须让第一层循环遍历背包，第二层循环遍历物品，这样才能考虑完每种物品作为最后一个的情况。

该题的中间结果大小会超过 int，LeetCode上会报错，所以需要加一个额外判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int combinationSum4(vector<int>& nums, int target)
{
    vector<int> dp(target+1, 0);
    dp[0] = 1;

    for (int i = 0; i <= target; i++)
    {
        for (int num : nums)
        {
            if (i - num >= 0 && dp[i] < INT_MAX - dp[i-num])
                dp[i] += dp[i-num];
        }
    }

    return dp[target];
}

322. 零钱兑换（Medium）

该题需要计算出打到总金额最少的硬币数为多少，可以分析出：

  • 背包大小：总金额
  • 物品：硬币
    • 重量：硬币面额
    • 价值：1（一枚硬币）
  • dp[i] ：表示总金额为 i 的最少硬币数

该题的初始化需要好好选择，如果初始化为 0 则后序判断比较麻烦，如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int coinChange(vector<int>& coins, int amount)
    {
        if (amount == 0) return 0;
        
        vector<int> dp(amount+1, 0);

        for (int& coin: coins)
        {
            for (int i = coin; i <= amount; i++)
            {
                if (dp[i-coin] == 0 && i > coin)		// 选取该硬币后达不到当前总金额
                    dp[i] = dp[i];
                else if (dp[i] != 0)					// 排除初始值为 0 的情况影响 min 函数
                    dp[i] = min(dp[i-coin] + 1, dp[i]);
                else
                    dp[i] = dp[i-coin] + 1;
            }
        }

        return dp[amount] == 0 ? -1 : dp[amount];
    }

实际上，如果把初始值设为最大值 INT_MAX，然后让 dp[0] = 0，就可以避免上述的复杂判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int coinChange(vector<int>& coins, int amount)
{
    if (amount == 0) return 0;

    vector<int> dp(amount+1, INT_MAX);
    dp[0] = 0;

    for (int& coin: coins)
    {
        for (int i = coin; i <= amount; i++)
        {
            if (dp[i-coin] != INT_MAX)
                dp[i] = min(dp[i-coin] + 1, dp[i]);
        }
    }

    return dp[amount] == INT_MAX ? -1 : dp[amount];
}

279. 完全平方数（Medium）

该题与 322. 零钱兑换 其实几乎一模一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int numSquares(int n)
{
    vector<int> dp(n+1, INT_MAX);
    dp[0] = 0;
    int sqrtN = (int) sqrt(n);

    for (int i = 1; i <= sqrtN; i++)
    {
        int square = i * i;
        for (int j = square; j <= n; j++)
        {
            if (dp[j-square] != INT_MAX)
                dp[j] = min(dp[j], dp[j-square] + 1);
        }
    }

    return dp[n];
}

139. 单词拆分（Medium）

  • 背包大小：目标串 s
  • 物品：单词
    • 重量：单词本身

如：applepenapple

  • dp[“”] = true
  • dp[“apple”] = dp[“apple” - “apple”] = dp[“”] = true;
  • dp[“applepen”] = dp[“applepen” - “pen”] = dp[“apple”] = true
  • dp[“applepenapple”] = dp[“applepenapple” - “apple”] = dp[“applepen”] = true;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool wordBreak(string s, vector<string>& wordDict)
{
    unordered_map<string, bool> dp;
    dp[""] = true;

    for (int i = 1; i <= s.size(); i++)
    {
        for (const string& word: wordDict)
        {
            if (word.size() <= i && s.substr(i - word.size(), word.size()) == word)
            {
                if (!dp[s.substr(0, i)])
                    dp[s.substr(0, i)] = dp[s.substr(0, i - word.size())];
            }
        }
    }

    return dp[s];
}
LeetCode题解
#算法题解
动态规划
http://blog.ashechol.top/posts/a80d0031.html
作者
Ashechol
发布于
2023年2月20日
许可协议