回溯

回溯

组合

77. 组合（Medium）

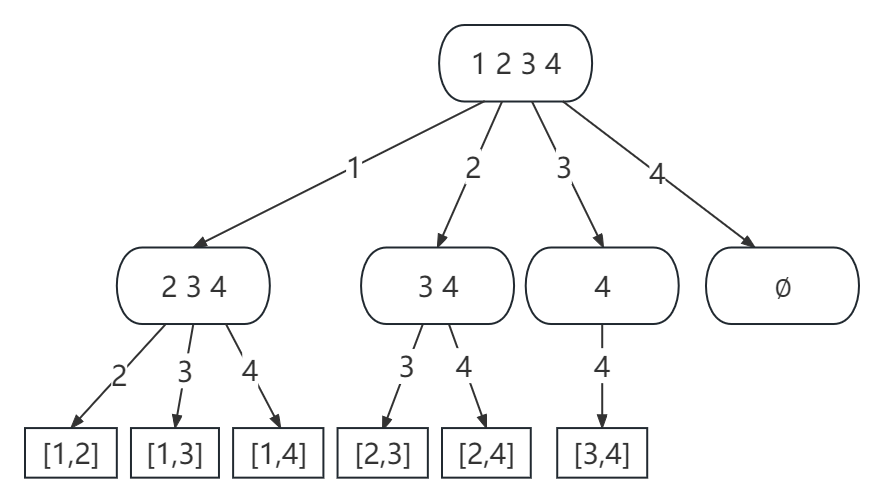
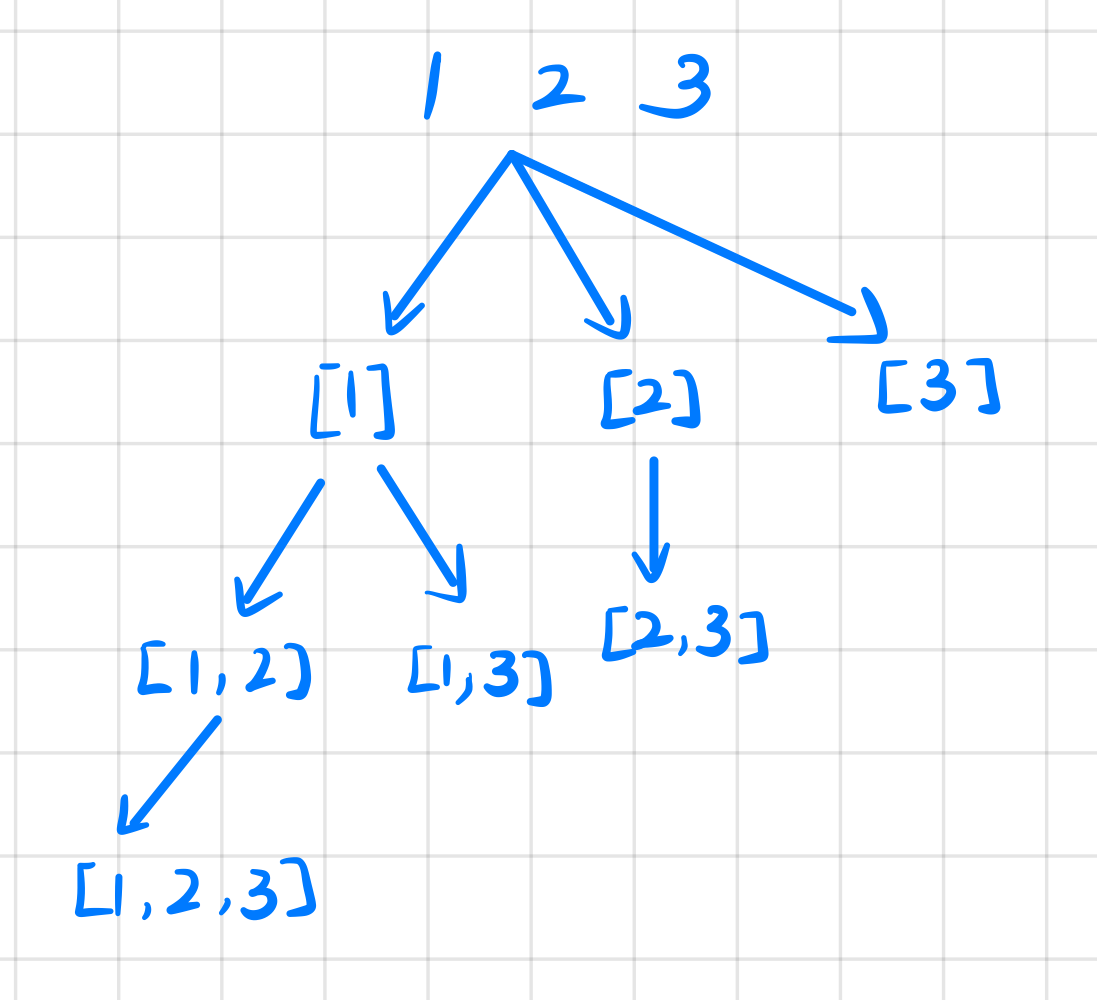
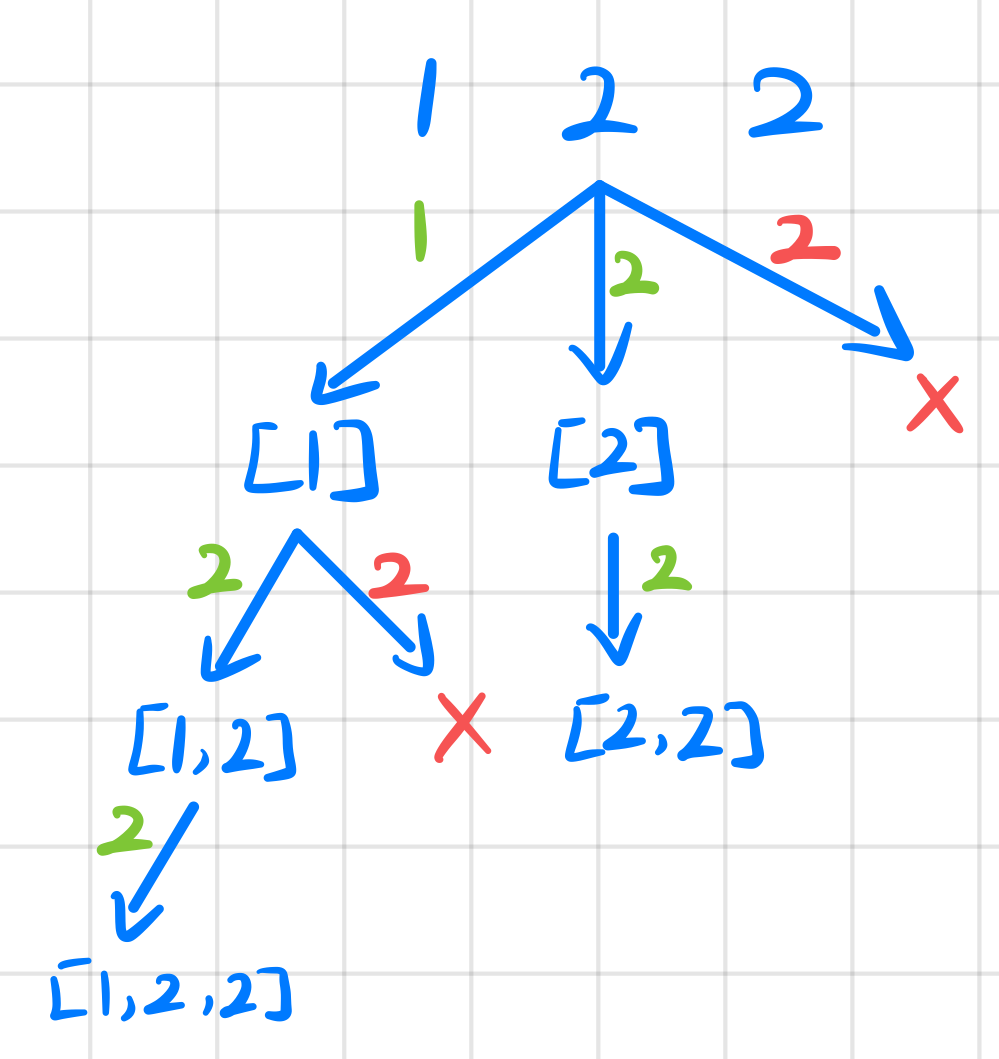
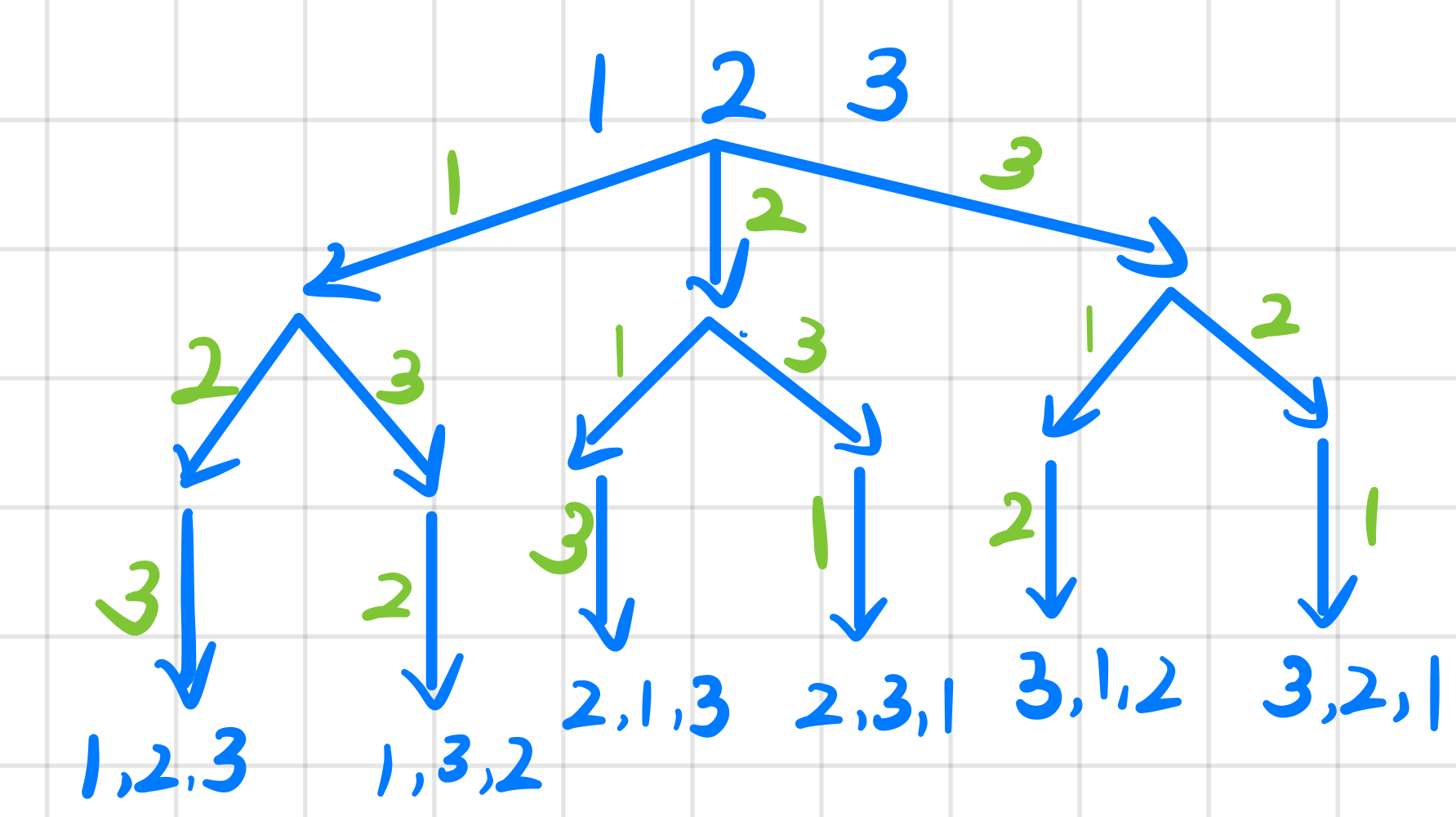
组合问题的可以用以下树形结构表示

这样就很容易写出其回溯代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
vector<vector<int>> ans;
vector<int> path;
void dfs(int bg, int n, int k)
{
    if (path.size() == k)
    {
        ans.emplace_back(path);
        return;
    }
    
    // 对于当前剩余数量少于所需数量的情况进行剪枝
    // n - i + 1 >= k - path.size()
    for (int i = bg; i <= n - (k - path.size()) + 1; i++)
    {
        path.emplace_back(i);
        dfs(i + 1, n, k);
        path.pop_back();
    }
}

vector<vector<int>> combine(int n, int k)
{
    dfs(1, n, k);
    return ans;
}

类似题目：

39. 组合总和（Medium）

因为允许重复使用元素，所以进入下一层递归就不需要缩小范围。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
vector<vector<int>> res;
vector<int> path;
int sum;

void dfs(vector<int>& nums, int bg, int target)
{
    if (sum == target)
    {
        res.emplace_back(path);
        return;
    }

    // if (sum > target) return;
    // 直接剪枝：在循环时就可以判断是否进入下层，但是需要提前排序
    for (int i = bg; i < nums.size() && sum + nums[i] <= target; i++)
    {
        path.emplace_back(nums[i]);
        sum += nums[i];
        dfs(nums, i, target);	// 下层的 bg 为 i，允许重复元素
        path.pop_back();
        sum -= nums[i];
    }
}

vector<vector<int>> combinationSum(vector<int>& candidates, int target) 
{
    sort(candidates.begin(), candidates.end());
    dfs(candidates, 0, target);
    return res;
}

40. 组合总和 II（Medium）

该题不能重复使用同一个元素，但是传入数组中有重复元素。为了避免出现重复的组合，首先对数组排序，然后跳过之前已经选中过的数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void dfs(vector<int>& nums, int bg, int target)
{
    if (sum == target)
    {
        res.emplace_back(path);
        return;
    }

    for (int i = bg; i < nums.size() && sum + nums[i] <= target; i++)
    {
        // 跳过本层已经选中过的重复元素
        if (i > bg && nums[i-1] == nums[i]) continue;

        path.emplace_back(nums[i]);
        sum += nums[i];
        dfs(nums, i+1, target);		// 缩小范围
        path.pop_back();
        sum -= nums[i];
    }
}

vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
    sort(candidates.begin(), candidates.end());
    dfs(candidates, 0, target);
    return res;
}

分割

131. 分割回文串（Medium）

分割

如上图所示，对于每一层的各种情况实际是从字符串长度为 1 开始遍历到整个字符串的过程。每一层的开始字符是上一层的结尾字符的后一个。所以不难写出回溯代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
vector<vector<string>> res;
vector<string> path;

void dfs(string& s, int bg)
{
    // 已经遍历完全部字符串
    if (bg == s.size())
    {
        res.emplace_back(path);
        return;
    }


    for (int i = bg; i < s.size(); i++)
    {	
        // 取子字符串，因为substr是用的字符个数n，而且是[bg, i]，所以需要 i-bg+1
        string tmp = s.substr(bg, i - bg + 1);
        if (check(tmp))
        {
            path.emplace_back(tmp);
            dfs(s, i+1);
            path.pop_back();
        }
    }
}

回文检测

该题另外一个重要的部分是回文字符串的判断。有很多方法可以实现。

判断倒置后是否与原本相同

1
2
3
4
5
6
bool check(string s)
{
    string rs = s;
    reverse(s.begin(), s.end());
    return s == rs;
}

首尾指针向内比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 对于子串
bool check(string s)
{
    for (int i = 0, j = s.size() - 1; i < j; i++, j--)
    {
        if (s[i] != s[j])
            return false;
    }
    return true;
}
// 或者通过子串下标
bool check(string s, int bg, int ed)
{
    int l = bg, r = ed;
    while (l < r)
    {
     	if (s[l++] != s[r--])
            return false;
    }
    return true;
}

记忆化搜索

因为判断一个字符串是否回文，其实就是判断，首尾字符是否相等以及中间的子串自否是回文字符串，所以可以通过二维数组记录 [bg, ed] 的字符串是否回文。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
vector<vector<int>> record;

// 0为未初始化 1为true 2位false
int check(string s, int bg, int ed)
{
    // 重复串，直接返回
    if (record[bg][ed] != 0)
        return record[bg][ed];

    for (int i = bg, j = ed; i < j; i++, j--)
    {
        // 首尾不等或者子串不是回文
        if (s[i] != s[j] || record[i+1][j-1] == 2)
        {
            record[bg][ed] = 2;
            return 2;
        }
		// 中间子串判断
        if (record[i+1][j-1] == 1)
        {
            record[bg][ed] = 1;
            return 1;
        }
    }
    record[bg][ed] = 1;
    return 1;
}

void dfs(string& s, int bg, vector<vector<string>>& res, vector<string>& path)
{
    if (bg == s.size())
    {
        res.emplace_back(path);
        return;
    }

    for (int i = bg; i < s.size(); i++)
    {
        if (check(s, bg, i) == 1)
        {
            path.emplace_back(s.substr(bg, i-bg+1));
            dfs(s, i+1, res, path);
            path.pop_back();
        }
    }
}

vector<vector<string>> partition(string s) 
{
    record.resize(s.size(),vector<int>(s.size(), 0));
    vector<vector<string>> res;
    vector<string> path;
    dfs(s, 0, res, path);
    return res;
}

93. 复原 IP 地址（Medium）

本体主要难点在于有很多种无效 IP 地址的情况需要分析：

  • 遍历完字符串没有 4 个整数
  • 有四个整数时没有遍历完字符串
  • 整数大于 255
  • 整数是有 0 开头

考虑到以上 4 点后，就可以写出正确的回溯

题目确保了不会有数字外的其他字符，所以不用考虑字符是否为数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
int cnt;
void dfs(const string& s, int bg, vector<string>&res, string path)
{
    // 遍历完字符串且有 4 个整数是正确答案
    if (bg == s.size() && cnt == 4)
    {
        path.pop_back();		// 删除多余的 '.'
        res.emplace_back(path);
        return;
    }
	// 剪枝：有四个整数时没有遍历完字符串
    if (cnt == 4 && bg < s.size())
        return;
	
    // 剪枝：每层最多往后遍历三个字符
    for (int i = bg; i < s.size() && i < bg + 3; i++)
    {
        string tmp = s.substr(bg, i-bg+1);
		
        // 剪枝：无效整数
        if (stoi(tmp) > 255 || (s[bg] == '0' && i > bg)) return;

        cnt++;
        dfs(s, i+1, res, path+tmp+'.'); // 直接把 path 放入形参回溯
        cnt--;
    }
}

vector<string> restoreIpAddresses(const string& s)
{
    vector<string> res;
    // 字符超过 12 个或者小于 4个 肯定不可能有正解
    if (s.size() > 12 || s.size() < 4) return res;

    dfs(s, 0, res, "");
    return res;
}

子集

78. 子集（Medium）

如上图，分析画出回溯树后不难通过代码实现。

子集和组合分割不同的地方在于，在终止判断前存入 path，否则会在终止时漏掉最后一个子集。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void dfs(vector<int>& nums, int bg, vector<vector<int>>& res, vector<int>& path)
{
    res.emplace_back(path);

    if (bg == nums.size())
        return;

    for (int i = bg; i < nums.size(); i++)
    {
        path.emplace_back(nums[i]);
        dfs(nums, i+1, res, path);
        path.pop_back();
    }
}

vector<vector<int>> subsets(vector<int>& nums) 
{
    vector<vector<int>> res;
    vector<int> path;
    dfs(nums, 0, res, path);
    return res;
}

90. 子集 II（Medium）

本体和 78. 子集 的不同之处是要排除重复的子集，比如，[1, 第一个2] 和 [1, 第二个2]。

从上图分析可以知道，判断是否重复实际是在递归的每层判断是否有重复的值。为此我们可以先讲输入排序，然后用 i 和 i - 1 对应的数来判断是否重复

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void dfs(vector<int>& nums, int bg, vector<vector<int>>& res, vector<int>& path)
{
    res.emplace_back(path);

    if (bg == nums.size())
        return;

    for (int i = bg; i < nums.size(); i++)
    {
        // 和上一个相同，跳过
        if (i > bg && nums[i] == nums[i-1])
            continue;

        path.emplace_back(nums[i]);                
        dfs(nums, i+1, res, path);
        path.pop_back();
    }
}

vector<vector<int>> subsetsWithDup(vector<int>& nums) {
    sort(nums.begin(), nums.end());
    vector<vector<int>> res;
    vector<int> path;
    dfs(nums, 0, res, path);
    return res;
}

491. 递增子序列（Medium）

该题因为要保证子集的递增，所以不能像 90. 子集 II 提前排序然后排除重复的数。

为此我们可以 利用哈希表来记录每个数 是否重复出现。

需要注意的是，重复的判断是针对与递归的每一层，所以每层需要一个单独的哈希表来记录。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
void dfs(vector<int>& nums, int bg, vector<vector<int>>& res, vector<int>& path)
{
    if (path.size() >= 2)
        res.emplace_back(path);

    if (bg == nums.size())
        return;
	
    // 记录该层的数，数的取值范围是[-100, 100]，所以可以开一个大小205的数组
    vector<bool> used(205, false);	
    for (int i = bg; i < nums.size(); i++)
    {
        // 重复的数跳过
        if (used[nums[i]+100])
            continue;
		
        // 满足递增的数加入子集
        if (path.empty() || nums[i] >= path.back())
        {
            path.emplace_back(nums[i]);
            used[nums[i]+100] = true;	// 这因为只针对该层，不能回溯
            dfs(nums, i+1, res, path);
            path.pop_back();
        }
    }
}

vector<vector<int>> findSubsequences(vector<int>& nums) {
    vector<vector<int>> res;
    vector<int> path;
    dfs(nums, 0, res, path);
    return res;
}

排列

46. 全排列（Medium）

在全排列问题中，因为顺序可以变，所以递归每一层的遍历都是从第一个数开始。

此外，我们需要避免重复选到已经用过的数。所以也需要通过哈希来记录 数的序号 。

需要注意的是，这里的哈希防止重复是针对纵向深度的，所以我们要把哈希表作为全局变量或者类变量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
vector<bool> used;	// 记录已经使用的数的序号
void dfs(vector<int>& nums, vector<vector<int>>& res, vector<int>& path)
{
    if (path.size() == nums.size())
    {
        res.emplace_back(path);
        return;
    }

    for (int i = 0; i < nums.size(); i++)
    {
        if (used[nums[i]+10])
            continue;

        path.emplace_back(nums[i]);
        used[nums[i]+10] = true;	// 因为是针对递归深度的记录，所以需要回溯
        dfs(nums, res, path);
        used[nums[i]+10] = false;
        path.pop_back();
    }
}
vector<vector<int>> permute(vector<int>& nums) {
    vector<vector<int>> res;
    vector<int> path;
    used.resize(25, false);
    dfs(nums, res, path);

    return res;
}

47. 全排列 II（Medium）

该题与 46. 全排列 不同之处在于会有重复元素。所以我们需要再纵向深度排除选到同一个位置数的同时，也要在每层横向排除重复的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
vector<bool> usedIndex;	// 纵向记录
void dfs(vector<int>& nums,vector<vector<int>>& res, vector<int>& path)
{
    if (path.size() == nums.size())
    {
        res.emplace_back(path);
        return;
    }

    vector<bool> usedVal(25, false);	// 横向记录
    for (int i = 0; i < nums.size(); i++)
    {
        if (usedIndex[i] || usedVal[nums[i]+10])
            continue;

        path.emplace_back(nums[i]);
        usedIndex[i] = true;
        usedVal[nums[i]+10] = true;
        dfs(nums, res, path);
        usedIndex[i] = false;
        path.pop_back();
    }
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
    vector<vector<int>> res;
    vector<int> path;
    usedIndex.resize(nums.size(), false);
    dfs(nums, res, path);

    return res;
}

图

332. 重新安排行程（Hard）

本题的主要难点在于如何设计一个数据结构来存储输入的每个地点之间的连通信息。

通常来说对于图问题，可以用一个二维数组来存储各节点之间的连通信息。但是该题要求如果有多个解返回字典序最小的组合。因此用二维数组不合适。

另一种方案是设计一个类似链表的结构体。

1
2
3
4
5
struct Node
{
    string name;
    vector<Node*> nexts; // nexts 里面存储按字典序排序的下个结点
};

但是这个方案，对于题目的输入信息并不好构建图，因为没有办法快速找到对应名字的节点。

既然要找对应名字，按照上面这种结构换一个思路，采用哈希表。

1
2
3
4
// 哈希表的 key 存储该节点的名字用于查询，value 存储指向飞往节点的名字
// 这里 value 用到了容器 map，用于将存储的地点名按照字典序排序
// 每张机票只能用一次（欧拉回路/路问题），而且可能会有重复的机票，所以 map 的 value 使用 int 来记录剩余数量。
unordered_map<string, map<string, int>> route;

确定好了合适的数据结构，接下来就不难写出带回溯的 dfs 函数了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
typedef unordered_map<string, map<string, int>> Route;
bool dfs(Route& route, vector<string>& res, int remain)
{
    // 机票用完就代表找到正确解了（因为我们优先找字典序小的节点）
    if (remain == 0) return true;
	
    // 键值不能修改，所以这里的 pair 引用的键值必须是 const string
    for (pair<const string, int>& to: route[res.back()])
    {
        // 去下个结点的机票用完的就跳过
        if (to.second == 0) continue;

        to.second--;
        res.emplace_back(to.first);
        if (dfs(route, res, remain-1))
            return true;
        res.pop_back();
        to.second++;
    }
    return false;
}
vector<string> findItinerary(vector<vector<string>>& tickets)
{
    vector<string> res;
    Route route;
	
    // 按照输入初始化哈希表
    for (const vector<string>& ticket: tickets)
        route[ticket[0]][ticket[1]]++;
	
    res.emplace_back("JFK");	// 起点是 JFK
    dfs(route, res, tickets.size());

    return res;
}

其他

51. N 皇后

N 皇后问题可以理解为，每层只放一个棋子，然后放之前检查列，两条斜线上是否有其他已放置的皇后。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// 如果有 Q 返回 true
bool checkQueen(vector<string>& board, int row, int col)
{
    int n = board.size();
    for (int i = row; i >= 0; i--)				// 列
        if (board[i][col] == 'Q') return true;

    int i = row, j = col;
    while (i >= 0 && j >= 0)					// 左上斜线
        if (board[i--][j--] == 'Q') return true;

    i = row; j = col;
    while (i >= 0 && j < n)						// 右上斜线
        if (board[i--][j++] == 'Q') return true;

    return false;
}

void dfs(vector<string>& board, int row, vector<vector<string>>& res)
{	
    // 每层都放下了棋子说明找到一个解
    if (row == board.size())
    {
        res.emplace_back(board);
        return;
    }

    for (int i = 0; i < board.size(); i++)
    {
        if (checkQueen(board, row, i))
            continue;

        board[row][i] = 'Q';
        dfs(board, row+1, res);
        board[row][i] = '.';
    }
}

vector<vector<string>> solveNQueens(int n)
{
    vector<string> board(n, string(n, '.'));
    vector<vector<string>> res;
    dfs(board, 0, res);
    return res;
}
LeetCode题解
#算法题解
回溯
http://blog.ashechol.top/posts/f92eff5d.html
作者
Ashechol
发布于
2023年2月19日
许可协议