重心坐标系推导

重心/质心坐标系（barycentric coordinate），是一个基础但十分重要的数学工具。他可以应用在三角形光栅化的内外像素点判断问题，以及进行重心插值（barycentric interpolation）

1. 推导

在一个平面上有三个点 \(p_0,p_1,p_2\) ，那么我们可以通过这三个点得到相邻的两个向量，而这两个向量和它们重合点的向量则可以线性表示该平面上的任意点。

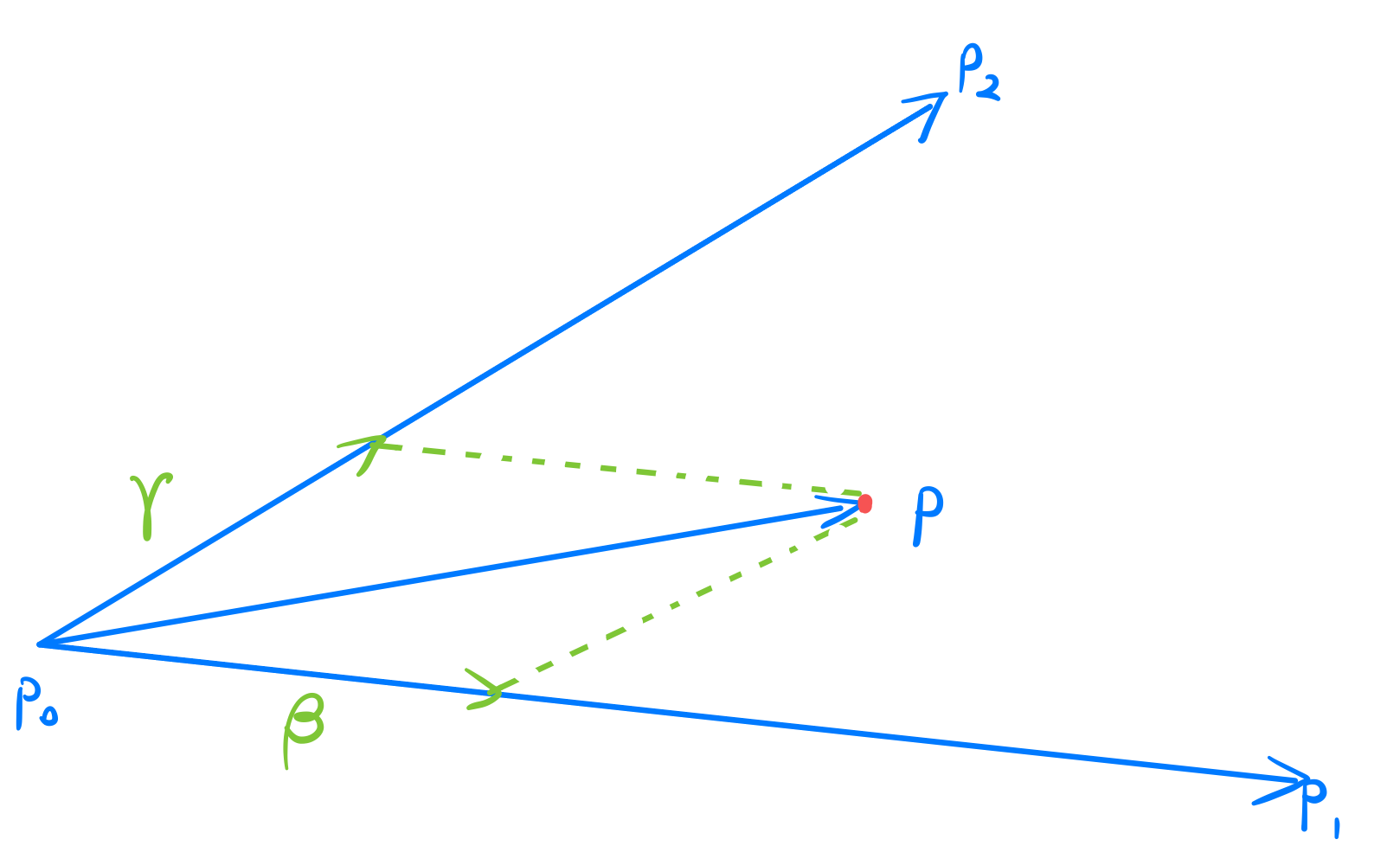
如上图所示，可以得到 \[ \boldsymbol p=\boldsymbol p_0 + \beta \cdot (\boldsymbol p_1-\boldsymbol p_0)+ \gamma\cdot (\boldsymbol p_2-\boldsymbol p_0) \] 整理得 \[ \boldsymbol p=(1-\beta-\gamma)\boldsymbol p_0+\beta\cdot\boldsymbol p_1+\gamma\cdot\boldsymbol p_2 \] 令 \[ \alpha=1-\beta-\gamma \]

得到 \[ \boldsymbol p(\alpha,\beta,\gamma)=\alpha\cdot\boldsymbol p_0+\beta\cdot\boldsymbol p_1+\gamma\cdot\boldsymbol p_2 \] 且约束条件为 \[ \alpha+\beta+\gamma=1 \] 这样就得到了基于三个参数 \(\alpha,\beta,\gamma\) 的重心坐标系。

2. 参数求解

2.1 带入全部点直接求解

三个参数可以通过带入点 \(p(x,y)\) 解如下方程得到： \[ \begin{cases} x=\alpha x_0+\beta x_1+\gamma x_2\\ y=\alpha y_0+\beta y_1+\gamma y_2\\ \gamma = 1-\alpha-\beta \end{cases} \] 得到 \[ \begin{cases} (x_0-x_2)\alpha+(x_1-x_2)\beta=x-x_2\\ (y_0-y_2)\alpha+(y_1-y_2)\beta=y-y_2 \end{cases} \]

\[ \begin{align} \mathbf D&=(x_0-x_2)(y_1-y_2)-(x_1-x_2)(y_0-y_2)\\ \mathbf D_\alpha&=(x-x_2)(y_1-y_2)-(x_1-x_2)(y-y_2)\\ \mathbf D_\beta&=(x_1-x_2)(y-y_2)-(x-x_2)(y_1-y_2) \end{align} \]

解得 \[ \alpha=\frac{\mathbf D_\alpha}{\mathbf D}=\frac{(x-x_2)(y_1-y_2)-(x_1-x_2)(y-y_2)}{(x_0-x_2)(y_1-y_2)-(x_1-x_2)(y_0-y_2)} \]

\[ \beta=\frac{\mathbf D_\beta}{\mathbf D}=\frac{(x_0-x_2)(y-y_2)-(x-x_2)(y_0-y_2)}{(x_0-x_2)(y_1-y_2)-(x_1-x_2)(y_0-y_2)} \]

\[ \gamma=1-\alpha-\beta \]

2.2 利用面积求解

如图所示

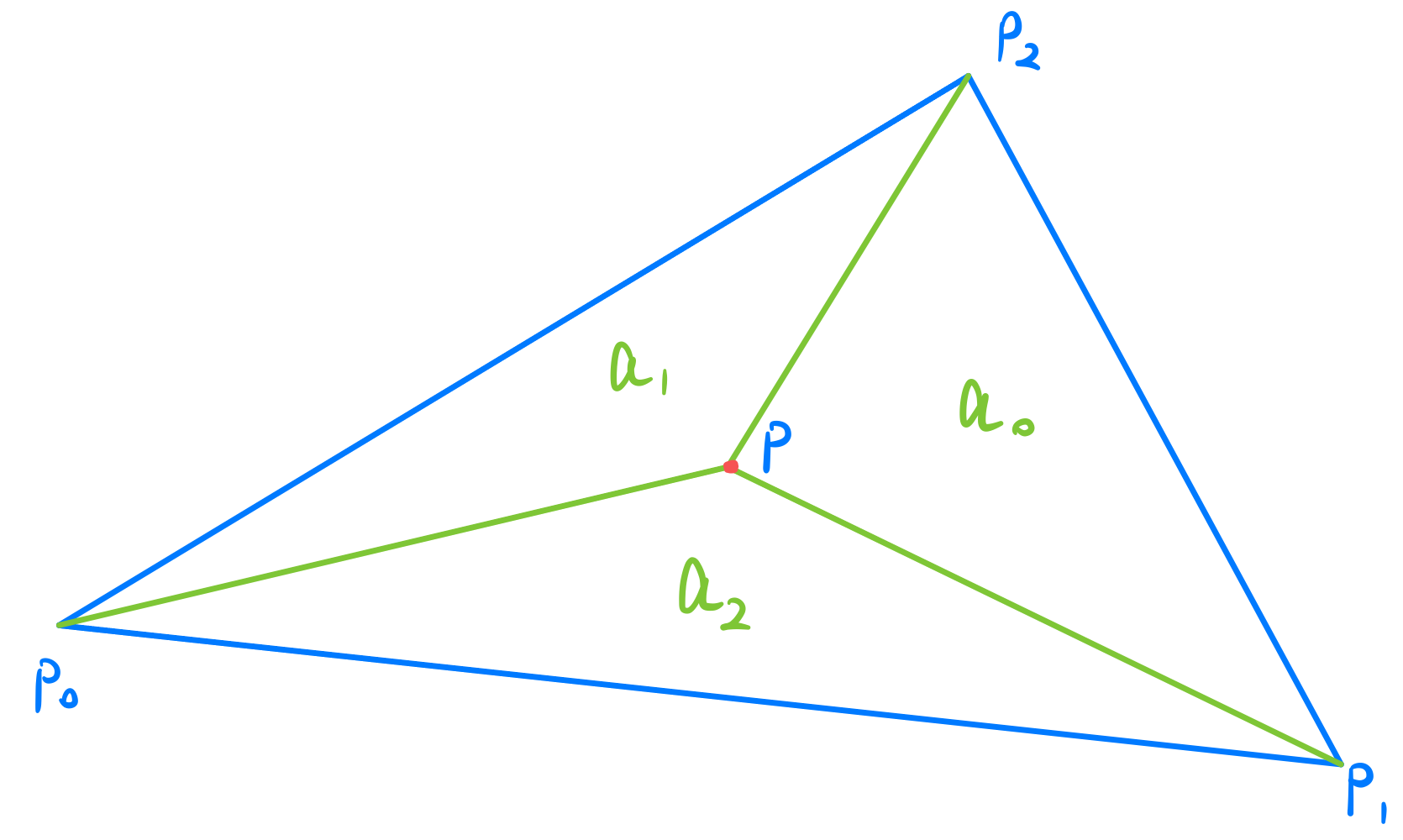
三个顶点与点 \(p\) 连线，形成了三个三角形。这三个三角形面积 \(a_0,a_1,a_2\) 和三角形 \(p_0p_1p_2\) 面积 \(a\) 之比即可算出 \(\alpha,\beta,\gamma\)。 \[ \alpha=\frac{a_0}{a}\ \ \beta=\frac{a_1}{a}\ \ \gamma=\frac{a_2}{a} \] 需要注意的是，为了满足 \(a_0+a_1+a_2=a\) ，当点 \(p\) 在三角形外，需要部分面积加上负号。

知道空间中任意三个点计算其构成的三角形面积，可以利用向量叉乘 \[ S_{\Delta}=\frac{1}{2}ab\sin\theta=\frac{1}{2}|\boldsymbol a||\boldsymbol b|\sin\theta =\frac{1}{2}|\boldsymbol a\times\boldsymbol b| \]