傅里叶变换和信号处理

1. 傅里叶变换

1.1 傅里叶级数

在解释傅里叶变换（Fourier transform）前，先要了解傅里叶级数（Fourier Series）。

傅里叶级数的思想是：任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。

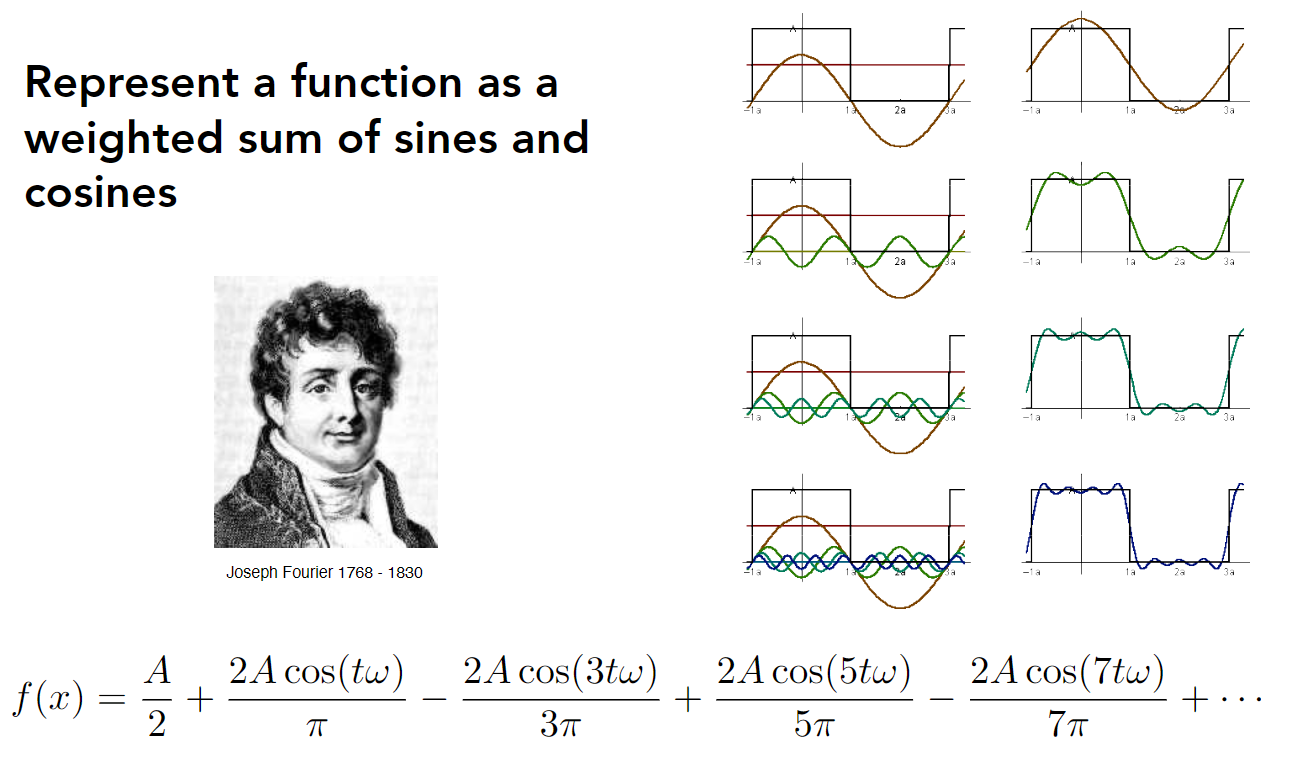
因为角速度 \(\omega=2\pi f\)

正弦函数和余弦函数的频率形式表示为： \[ \begin{align} \sin\omega t&=\sin2\pi ft\\ \cos\omega t&=\cos2\pi ft \end{align} \] 由此可以看出傅里叶级数实际上是用各种 频率 的正余弦函数相加来表示任意函数的。而频率对于人们研究信号是十分重要的一个指标。

信号可以看做一个连续的函数

1.2 傅里叶变换

那么有没有什么办法一次性获得任意函数的分解成傅里叶级数后的频率信息呢？答案是傅里叶变换。

傅里叶变换的本质是将一个函数（信号）在 时域（time domain）的表示转换为在 频域（frequency domain）的表示。

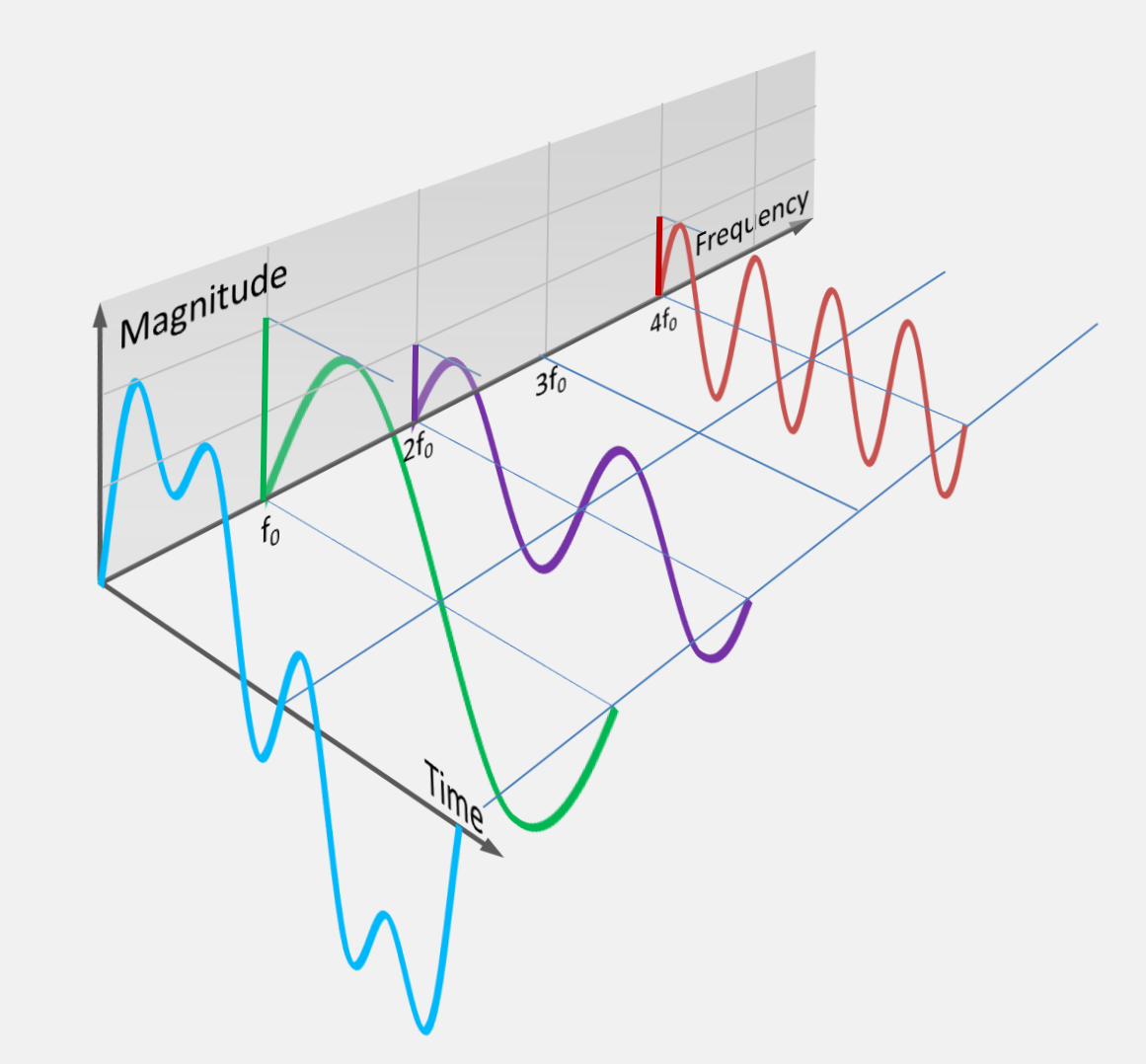
一个函数 \(Y(t)\) 和其傅里叶变换后的函数 \(F(f)\) 的关系如下，即傅里叶转换公式 \[ F(f)=\int^{+\infty}_{-\infty}Y(t)e^{-2\pi ift}\,dt \] 逆傅里叶转换公式如下 \[ Y(t)=\int_{-\infty}^{+\infty}F(f)e^{2\pi ift}\,df \] 其中 \[ e^{2\pi ift}=\cos2\pi ft+i\sin2\pi ft \]

2. 信号处理

这里主要讨论傅里叶变换在图像处理中的应用。对于二维图像，傅里叶变换不再是将信号从时域转换为频域，而是从空间域（spatial domain）转换为频域。

2.1 滤波

利用傅里叶变换，我们可以分析信号的频域信息，并对其进行操作（如过滤掉低频或者高频），然后再逆傅里叶变换回原始信号，从而实现对信号的处理。

如上所示，对左灰度图进行傅里叶变换后可以得到右图。二维图像傅里叶变换后得到的频域图像的像素越往中心则说明其频率越低，反之越高。

对于图像来说，频率越高说明像素的变化越明显，换句话来说，图像的频域信息高频部分代表了图像的细节信息（如边界）。如果我们去掉中心的低频信息则可以得到

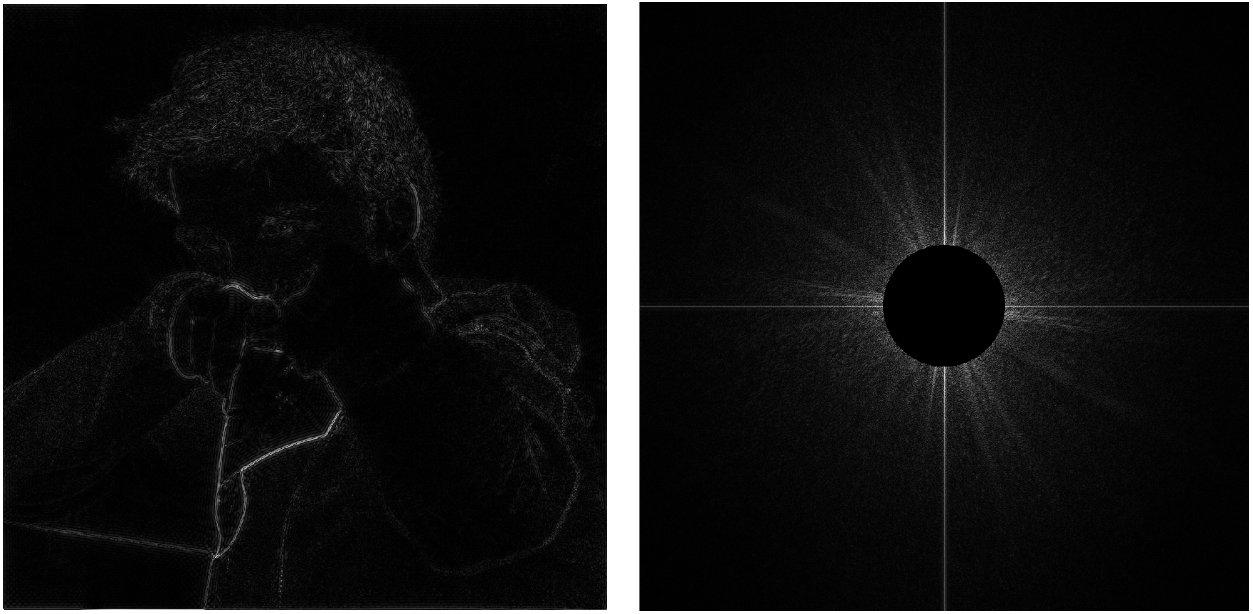
以上操作被称作 高通滤波（hight-pass filter）。

反之如果我们滤掉高频信息，则可以得到一个模糊的图像

这被称作 低通滤波（low-pass filter）。

2.2 卷积和滤波

卷积和傅里叶变换有以下性质：

• 两个函数在时域上的卷积等同于将两者傅里叶变换后在频域上的相乘
• 两个函数在时域上的相乘等同于将两者傅里叶变换后在频域上的卷积

由此我们可以知道，我们对一个图像进行卷积操作，同样可以达到滤波器的效果

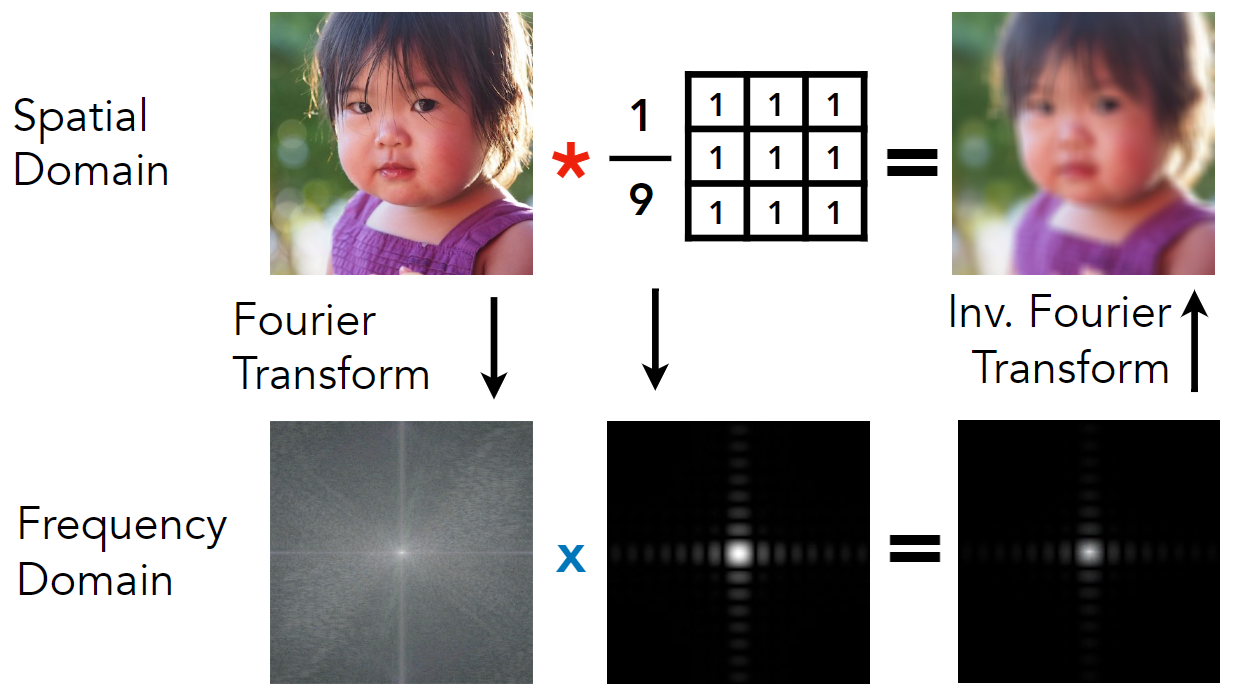
3. 混叠（Aliasing）

对于信号的采样可以表示为对信号函数乘以一个脉冲函数，如下所示

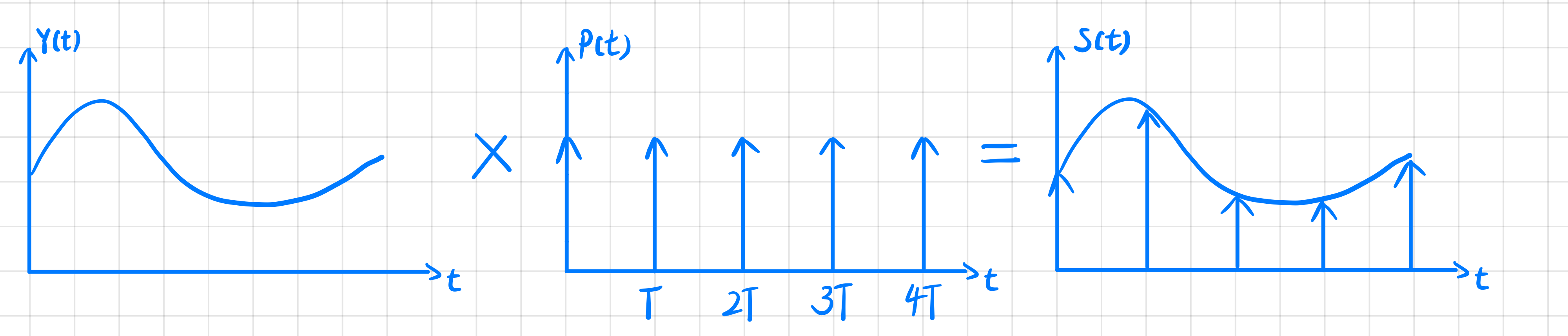
他们在频域上表示为卷积

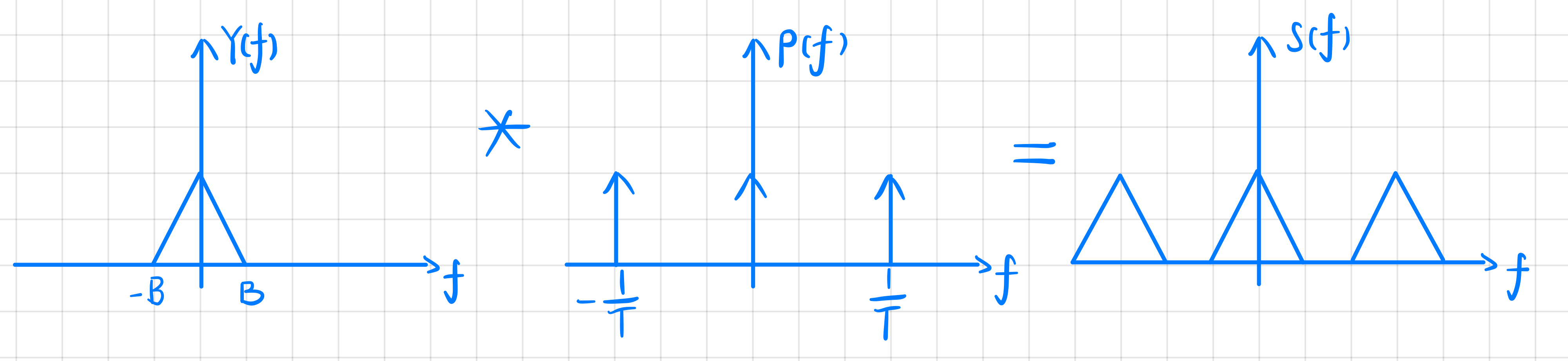
脉冲函数在频域下仍为一个脉冲函数，其周期为时域下周期的倒数，即采样率 \(f_s\)。而周期 \(T\) 越大，在频域上采样率就会越小，其间隔就会越小。

可以看到两者在频域的卷积实际上是将信号函数按照脉冲函数的周期在频域上重复。当脉冲函数在频域上的周期变小就会导致混叠现象。

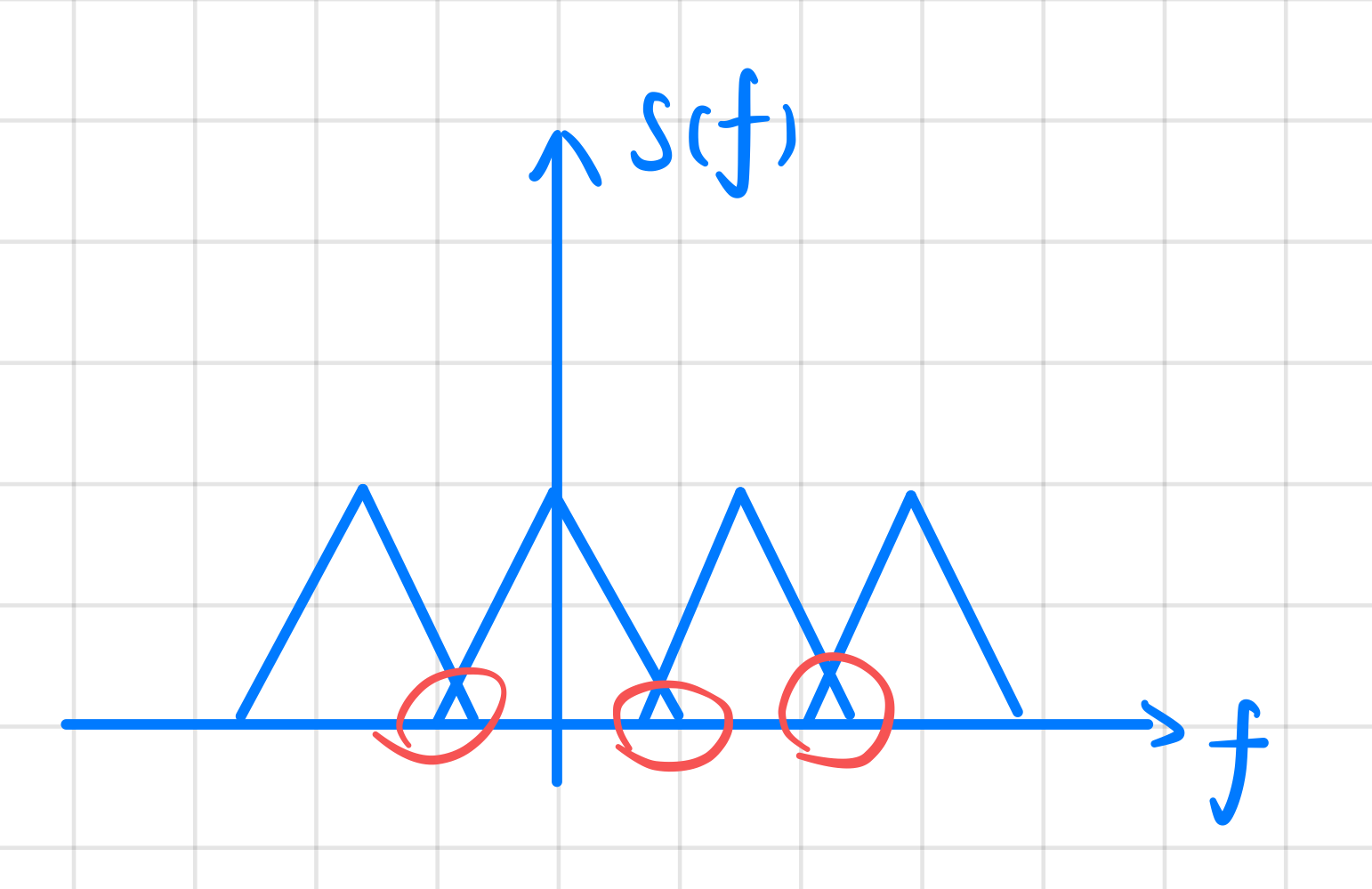
所以采样率越小就会更容易导致的混叠现象进而导致信号失真。

为了避免混叠，脉冲函数的采样率应该满足 \[ f_s\geqslant 2B \] \(2B\) 为被采样的信号在频域上的频谱宽度（最高频率的两倍）。这个不等式也被称作 奈奎斯特率（Nyquist rate）