二分查找

二分查找

704. 二分查找（Easy）

二分查找的容易出错的地方主要在边界的判定。不同判定方法的条件不同。

  • 左闭右闭

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    int search(vector<int>& nums, int target)
    {
        int left = 0, right = nums.size() - 1; // 右闭
        
        // 左闭右闭 left <= right
        while(left <= right)
        {
            int mid = left + ((right - left) >> 1);
        
            if (nums[mid] == target) return mid;
            if (nums[mid] < target) left = mid + 1;
            
            if (nums[mid] > target) right = mid - 1; // 右闭
        }
        
        return -1;
    }

  • 左闭右开

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    int search(vector<int>& nums, int target)
    {
        int left = 0, right = nums.size(); // 右开
        
        // 左闭右开 left < right
        while(left < right)
        {
            int mid = left + ((right - left) >> 1);
        
            if (nums[mid] == target) return mid;
            if (nums[mid] < target) left = mid + 1;
            
            if (nums[mid] > target) right = mid; // 右开
        }
        
        return -1;
    }

35. 搜索插入位置（Easy）

先二分查找，如果找到则返回下标，没有找到需要分二分区间情况来处理

  • 左闭右闭

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    int searchInsert(vector<int>& nums, int target)
    {
        int left{0}, right{ static_cast<int>(nums.size()) - 1 };

        while (left <= right)
        {
            int mid = ((right - left) >> 1) + left;

            if (nums[mid] == target) return mid;
            if (nums[mid] > target) right = mid - 1;
            if (nums[mid] < target) left = mid + 1;
        }

        return right + 1; // 右闭
    }

  • 左闭右开

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    int searchInsert(vector<int>& nums, int target)
    {
        int left{0}, right{ static_cast<int>(nums.size()) };

        while (left < right)
        {
            int mid = ((right - left) >> 1) + left;

            if (nums[mid] == target) return mid;
            if (nums[mid] > target) right = mid;
            if (nums[mid] < target) left = mid + 1;
        }

        return right; // 右开
    }

34. 在排序数组中查找元素的第一个和最后一个位置（Medium）

从目标向两边二分

先用一次二分查找找到目标，然后一目标为基准向两边二分找到左右边界。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// 二分查找（左闭右开）
int search(vector<int>& nums, int target, int left, int right)
{
    while (left < right)
    {
        int mid = ((right - left) >> 1) + left;

        if (nums[mid] == target) return mid;
        if (nums[mid] < target) left = mid + 1;
        if (nums[mid] > target) right = mid;
    }

    return -1;
}

vector<int> searchRange(vector<int>& nums, int target)
{
    int bg, ed;
    int left{0}, right{ static_cast<int>(nums.size()) };
    bg = ed = search(nums, target, left, right);

    if (bg == -1) return {-1, -1};
  
    // 对目标值左进行二分查找
    // 当找到的目标其左值不为目标值即为起始点
    while (bg - 1 >= left && nums[bg - 1] == target)
    {
        bg = search(nums, target, left, bg);
    }
    
    // 对目标值右进行二分查找
    // 当找到的目标其右值不为目标值即为终点
    while (ed + 1 < right && nums[ed + 1] == target)
    {
        ed = search(nums, target, ed + 1, right);
    }

    return {bg, ed};
}

两次二分找到左右边界

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int binarySearchBorder(vector<int>& nums, int target, bool l)
{
    int left = 0, right = nums.size() - 1;
    int res;

    while (left <= right)
    {
        int mid = left + ((right - left) >> 1);
		
        // 如果 l = true, 找左边界，不断收缩右边界
        if (nums[mid] > target || (l && nums[mid] == target))
        {
            right = mid - 1;
            // 更新左边界
            if (l) res = right;
        }
		
        // 如果 l = false, 找右边界，不断收缩左边界
        if (nums[mid] < target || (!l && nums[mid] == target))
        {
            left = mid + 1;
            // 更新右边界
            if (!l) res = left;
        }
    }

    return res;
}

vector<int> searchRange(vector<int>& nums, int target)
{
    int bg = binarySearchBorder(nums, target, true) + 1;
    int ed = binarySearchBorder(nums, target, false) - 1;

    if (bg <= ed && ed < nums.size() && nums[bg] == target)
        return {bg, ed};

    return {-1, -1};
}

69. x 的平方根（Easy）

求平方根可以用二分法或牛顿迭代法

二分法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int mySqrt(int x)
{
    double left{0}, right{ x * 1.0 };
    double mid{0};

    if (x == 1) return 1;

    while (abs(mid * mid - x) >= 0.01)
    {
        mid = ((right - left) * 0.5) + left;
        
        // cout << mid << endl;

        if (mid * mid == x) return static_cast<int>(mid);
        if (mid * mid < x) left = mid;
        if (mid * mid > x) right = mid;
    }

    return static_cast<int>(mid);
}

牛顿迭代法

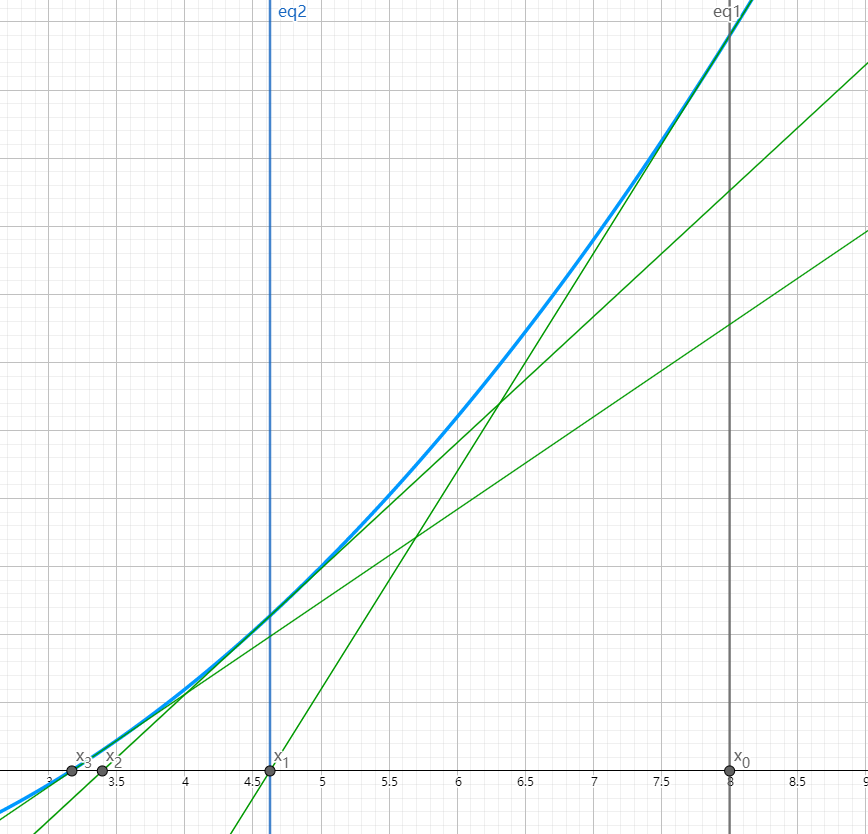
如上图所示，牛顿迭代法就是通过不断的求函数切线的零点，不断逼近函数的零点。

题目中求平方根可以转换为函数\(f(x)=x^2-C\)（C为被开根的值）

可以得到迭代公式：

\[ x_{k+1}=\frac{1}{2}(x_k+\frac{C}{x_k}) \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int mySqrt(int x)
{
    if (x == 0) return 0;

    double current{x * 1.0}, C{x * 1.0};

    while (true)
    {
        double next = 0.5 * (current + C / current);

        if (abs(current - next) < 1e-5) return static_cast<int>(current);

        current = next;
    }
}

367. 有效的完全平方数（Easy）

思路

开根取整，然后用 num除以该值，如果能整除即为true

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>

using namespace std;

bool isPerfectSquare(int num);
int mySqrt(int num);

int main()
{
    int num;
    cin >> num;
    cout << isPerfectSquare(num) << endl;
    return 0;
}

bool isPerfectSquare(int num)
{
    float x{static_cast<float>(mySqrt(num))};
    
    // 因为x取值范围很大，x*x会超过int范围，所以用除
    return static_cast<float>(num) / x == x; 
}

// 二分法求根
int mySqrt(int num)
{
    int left{0}, right{num};

    if (num == 1) return 1;

    while (left < right)
    {
        int mid = ((right - left) >> 1) + left;

        if (num / mid > mid) left = mid + 1;
        else right = mid;
    }

    return left;
}

33. 搜索旋转排序数组（Medium）

题目大意

搜索一个局部有序的数组，要求时间复杂度为 \(\log n\)

思路

不断的队数组进行二分，最后在有序的部分进行二分查找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
int search(vector<int>& nums, int target)
{
    int left = 0, right = nums.size();
	
    // 左闭右开
    while (left < right)
    {
        int mid = left + ((right - left) >> 1);

        if (nums[mid] == target) return mid;
		
        // [left, mid] 有序
        if (nums[left] <= nums[mid])
        {
            // target 在 [left, mid) 之间
            if (nums[left] <= target && target < nums[mid])
                right = mid;
            else
                left = mid + 1;
        }
        // [mid, right-1] 有序
        else
        {
            // target 在 (mid, right-1] 之间
            if (nums[mid] < target && target <= nums[right-1])
                left = mid + 1;
            else
                right = mid;
        }
    }

    return -1;
}
LeetCode题解 > 数组
#算法题解
二分查找
http://blog.ashechol.top/posts/e8eb0481.html
作者
Ashechol
发布于
2023年1月29日
许可协议