双指针

双指针

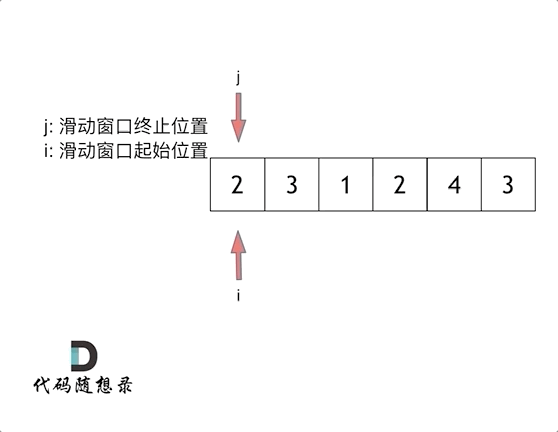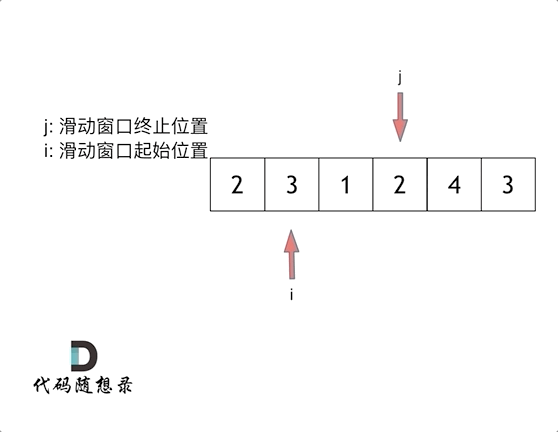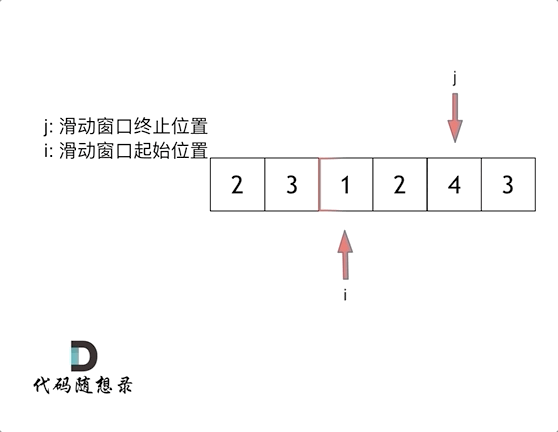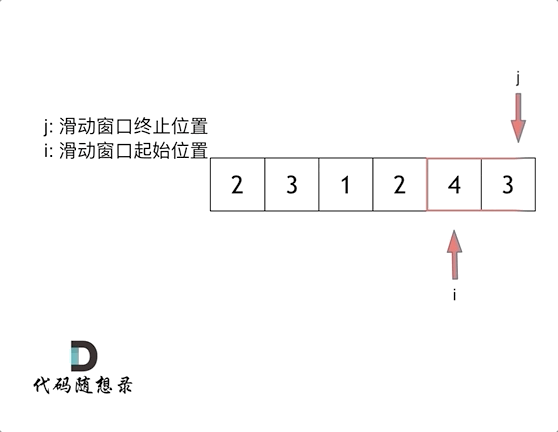
滑动窗口

209. 长度最小的子数组（Medium）

队列

  • 时间复杂度：\(O(n)\)
  • 空间复杂度：$ O(n) $

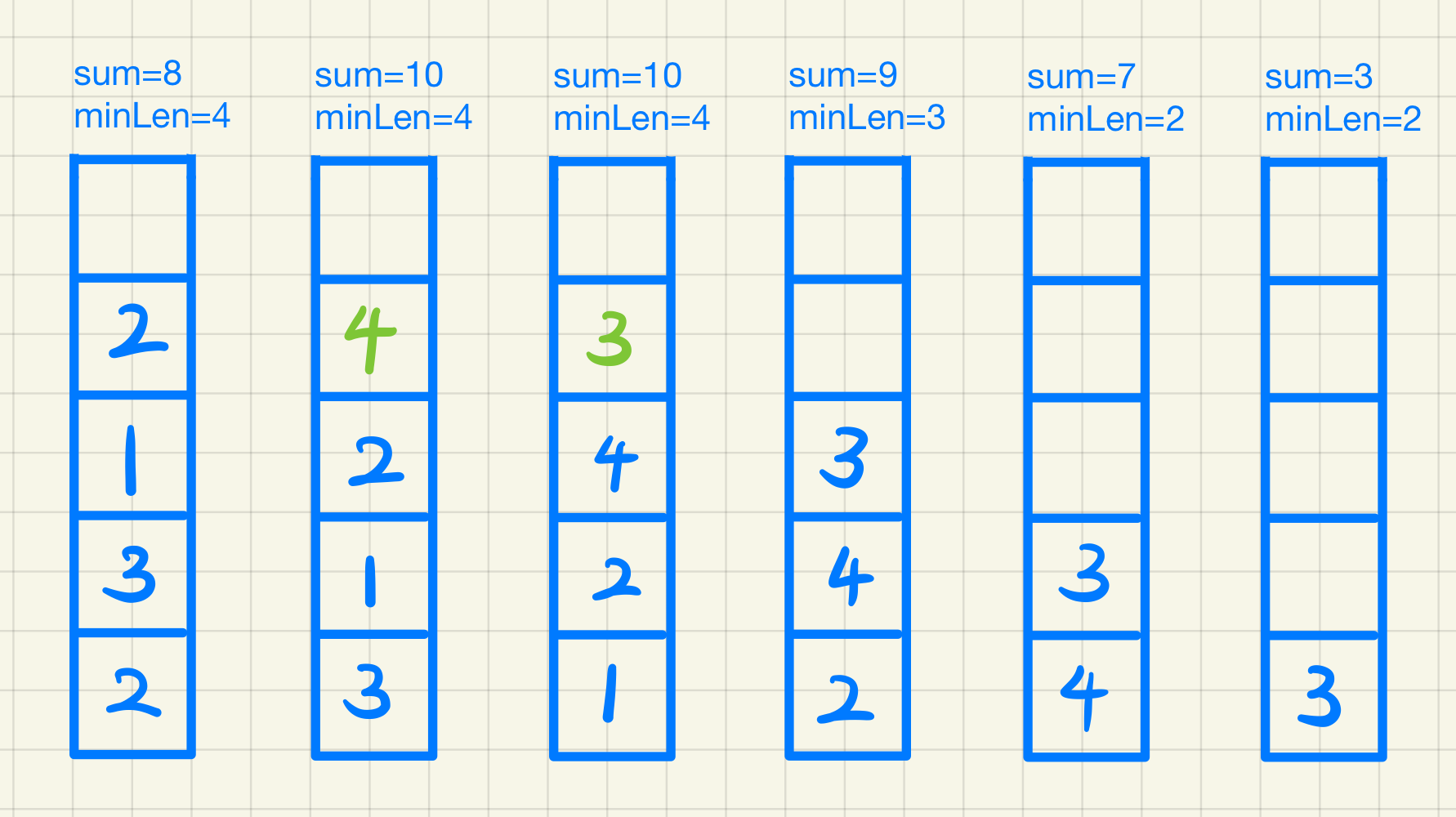
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int minSubArrayLen_que(int target, vector<int>& nums)
{
    queue<int> que;
        int sum = 0;
        int minLen = INT32_MAX;
        
        for (int& num: nums)
        {
            sum += num;
            que.push(num);

            while (sum >= target)
            {
                if (minLen > que.size()) minLen = (int) que.size();

                sum -= que.front();
                que.pop();
            }
        }

        return minLen == INT32_MAX ? 0 : minLen;
}

滑动窗口

  • 时间复杂度：\(O(n)\)
  • 空间复杂度：$ O(1) $

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
int minSubArrayLen(int target, vector<int>& nums)
{
    int sum = 0;
    int minLen = INT32_MAX;

    for (int l = 0, r = 0; r < nums.size(); r++)
    {
        sum += nums[r];

        while (sum >= target)
        {
            // r - l + 1 因为 [l, r]
            if (minLen > r - l + 1) minLen = r - l + 1;

            sum -= nums[l++];
        }
    }
    
    // 另外一种循环写法
    // for (int l = 0, r = 0; r < nums.size() || sum >= target;)
    // {
    //     if (sum >= target)
    //     {
               // [l, r)
    //         if (minLen > r - l) minLen = r - l;
    //
    //         sum -= nums[l++];
    //     }
    //     else if (r < nums.size())
    //         sum += nums[r++];
    // }

    return minLen == INT32_MAX ? 0 : minLen;
}

904. 水果成篮（Medium）

题目实际是求一个数组中，有最多两种不同值的最大连续子数组。所以可以使用滑动窗口来解决。

需要注意的是滑动窗口左边界的更新方式，比如：

1
2
1 2 1 2 2 2 3 3
其中 2 3 交界，左边界应该从 0 更新到 3，而不是 1 或者 5

滑动窗口 + 向左更新左边界

  • 时间复杂度：\(O(m+n)\approx O(n),\; m<n\)
  • 空间复杂度：\(O(1)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int totalFruit(vector<int>& fruits)
{
    int maxTotal = 0;
    // 当前子数组中水果种类，有先后顺序
    int fruitTypes[] = {-1, -1};

    if (fruits.size() <= 2) return (int) fruits.size();

    for (int l = 0, r = 0; r < fruits.size(); r++)
    {
        // 没有水果则加入
        if (fruitTypes[0] == -1)
            fruitTypes[0] = fruits[r];
        else if (fruitTypes[1] == -1 && fruitTypes[0] != fruits[r])
            fruitTypes[1] = fruits[r];
        // 有新的种类水果
        else if (fruitTypes[0] != fruits[r] && fruitTypes[1] != fruits[r])
        {
            // 有新的水果，则一定是交界，符合下面的规则
            fruitTypes[0] = fruits[r - 1];
            fruitTypes[1] = fruits[r];
            
            // 向左更新左边界，找到最大连续，种类为fruitType[0]的水果
            l = r;
            while (fruits[l - 1] == fruitTypes[0]) l--;
        }

        if (maxTotal < r - l + 1) maxTotal = r - l + 1;
    }

    return maxTotal;
}

滑动窗口+哈希表（unordered_map）/字典（map）

  • 时间复杂度：\(O(m+n)\approx O(n),\; m < n\)
  • 空间复杂度：$ O(n) $

使用一个哈希表或者字典，记录子数组水果种类和其数量。

当水果种类超过两种，则开始更新左边界：

  • 不断减去左边界对应水果的数量，并让左边界向右移动。
  • 当左边界对应的水果数量减少为0，则表示已经找到最新的左边界了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int totalFruit_Hashmap(vector<int>& fruits)
{
    int maxTotal = 0;
    unordered_map<int, int> fruitTypeNum;

    for (int l = 0, r = 0; r < fruits.size(); r++)
    {
        fruitTypeNum[fruits[r]]++;
        
        // 子数组水果种类超过2
        while (fruitTypeNum.size() > 2)
        {
            // 左指针对应水果种类的数量减少
            fruitTypeNum[fruits[l]]--;

            if (fruitTypeNum[fruits[l]] == 0)
                fruitTypeNum.erase(fruits[l]);
            
            // 左指针向右移动
            l++;
        }

        maxTotal = max(maxTotal, r - l + 1);
    }

    return maxTotal;
}

76. 最小覆盖子串（Hard）

滑动窗口+哈希表

  • 时间复杂度：\(O(m+n)\approx O(n),\; m<n\)
  • 空间复杂度：\(O(n)\)

方法一

  1. 首先，因为要对字符串中的各个字符的数量进行数量的比较，所以使用两个哈希表进行记录。
  2. 右指针遍历字符串的同时，更新哈希表中字符数量。
  3. 使用变量typeNum 对满足条件的字符种类进行统计。
  4. 当typeNum 大小为字符串t 哈希表的大小时，说明找到一个覆盖子串。
  5. 比较长度，如果是最小子串则更新结果。
  6. 开始对左边界更新，直到不满足覆盖条件。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
string minSubString(string s, string t)
{
    unordered_map<char, int> sCharCnt, tCharCnt;
    int minLen = INT32_MAX;
    string res;

    for (const char c: t) tCharCnt[c]++;

    int typeNum = 0;

    for (int l = 0, r = 0; r < s.size(); r++)
    {
        sCharCnt[s[r]]++;
        
        // 当前字符属于t，切数量等于t中的数量
        if (tCharCnt.find(s[r]) != tCharCnt.end() && sCharCnt[s[r]] == tCharCnt[s[r]])
            typeNum++;
        
        // 已满足覆盖条件
        while (typeNum == tCharCnt.size())
        {
            // 更新结果
            if (minLen > r - l + 1)
            {
                minLen   = r - l + 1;
                res = s.substr(l, r - l + 1);
            }
            
            // 左边界对应字符数量不等于t中的数量时，退出循环
            if (tCharCnt.find(s[l]) != tCharCnt.end() && --sCharCnt[s[l]] < tCharCnt[s[l]] )
                typeNum--;
            // 向右更新左边界
            l++;
        }
    }

    return res;
}

更为简洁的一种方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
string minSubString_abbr(string s, string t)
{
    unordered_map<char, int> sCharCnt, tCharCnt;
    string res;
    
    for (char c: t) tCharCnt[c]++;

    for (int l = 0, r = 0, cnt = 0; r < s.size(); r++)
    {
        sCharCnt[s[r]]++;
        
        // 更新为t中字符的总量
        if (sCharCnt[s[r]] <= tCharCnt[s[r]]) cnt++;
        
        // 向右更新左边界
        while (sCharCnt[s[l]] > tCharCnt[s[l]]) sCharCnt[s[l++]]--;
        
        // cnt == t.length 说明找到一个覆盖子串
        // 结果为空或者结果长度大于当前子串，则更新结果
        if (cnt == t.length() && (res.empty() || res.length() > r - l + 1))
            res = s.substr(l, r - l + 1);
    }

    return res;
}

这个方法的妙处就是，不去考虑种类的数量。而是统计s子串中，属于t的数量。

由于stl哈希表的特点：tCharCnt[s[r]] 如果tCharCnt 中没有键值为s[r] 的变量，

会创建一个{s[r], 0} 。

因此sCharCnt[s[r]] <= tCharCnt[s[r]] 仍然可以筛选掉不属于tCharCnt的键。

sCharCnt[s[l]] > tCharCnt[s[l]] 同理。

3. 无重复字符的最长子串（Medium）

使用哈希表存储出现过的字符，利用滑动窗口的左右指针来得到无重复字符串的长度，然后记录最小的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int lengthOfLongestSubstring(const string& s)
{
    int left = 0, right = 0;
    int res = 0;
    unordered_map<char, int> hash;

    while (right < s.length())
    {
        hash[s[right++]]++;
		
        // 如果当前字符重复了，则需要缩小左边界
        // 因为 right 自增了，需要减一得到当前记录的
        while (hash[s[right - 1]] > 1)
            hash[s[left++]]--;

        if (right - left > res)
            res = right - left;
    }

    return res;
}

快慢指针

27. 移除元素（Easy）

暴力法

  • 时间复杂度：$ O(n^2) $
  • 空间复杂度：$ O(1) $

每删除一个目标值，就将其之后的全部值向前覆盖。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int removeElement_brute(vector<int>& nums, int val)
{
    int length = static_cast<int>(nums.size());

    for (int i = 0; i < length; i++)
    {
        if (nums[i] == val)
        {
            for (int j = i; j < length - 1; j++)
                nums[j] = nums[j+1];

            length--;
            i--;
        }
    }

    return length;
}

快慢指针法

  • 时间复杂度：$ O(n) $
  • 空间复杂度：\(O(1)\)

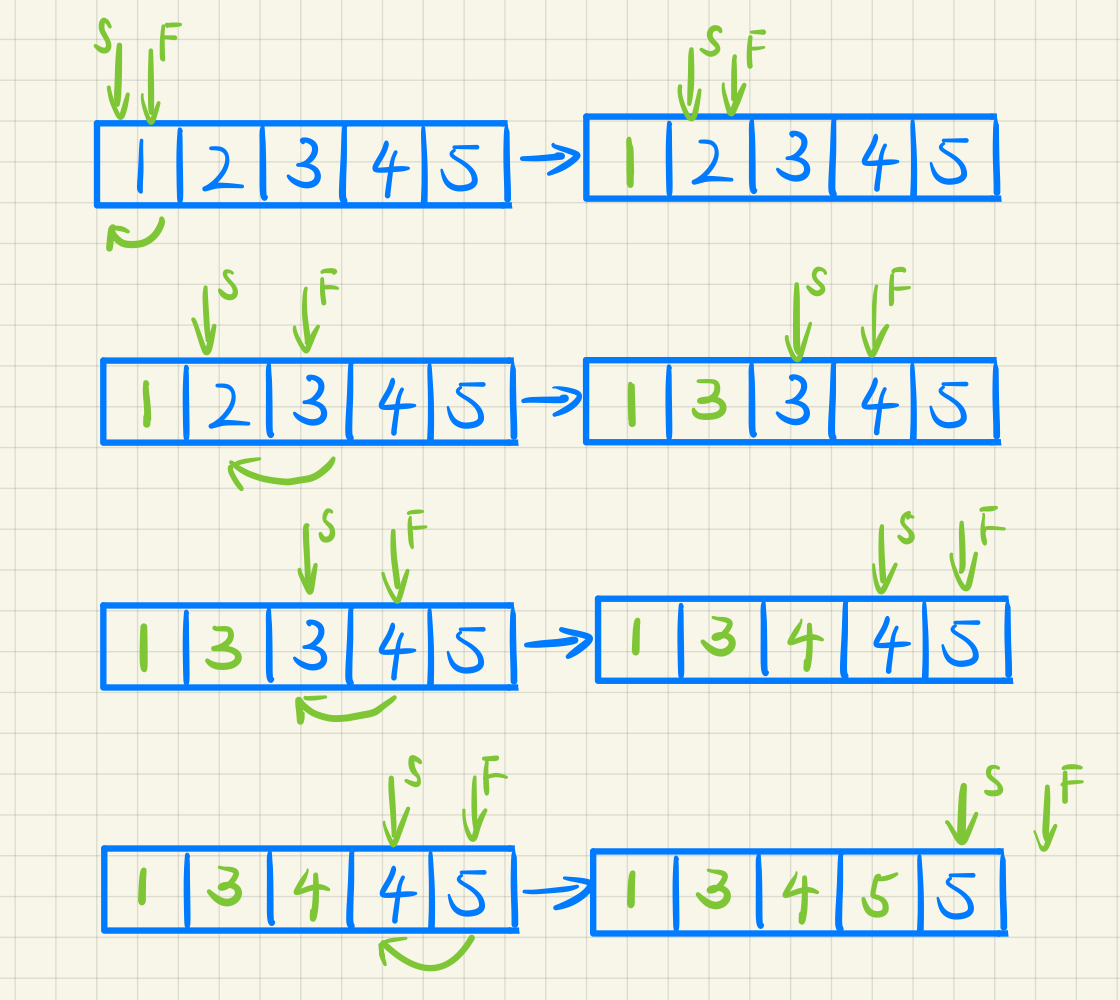
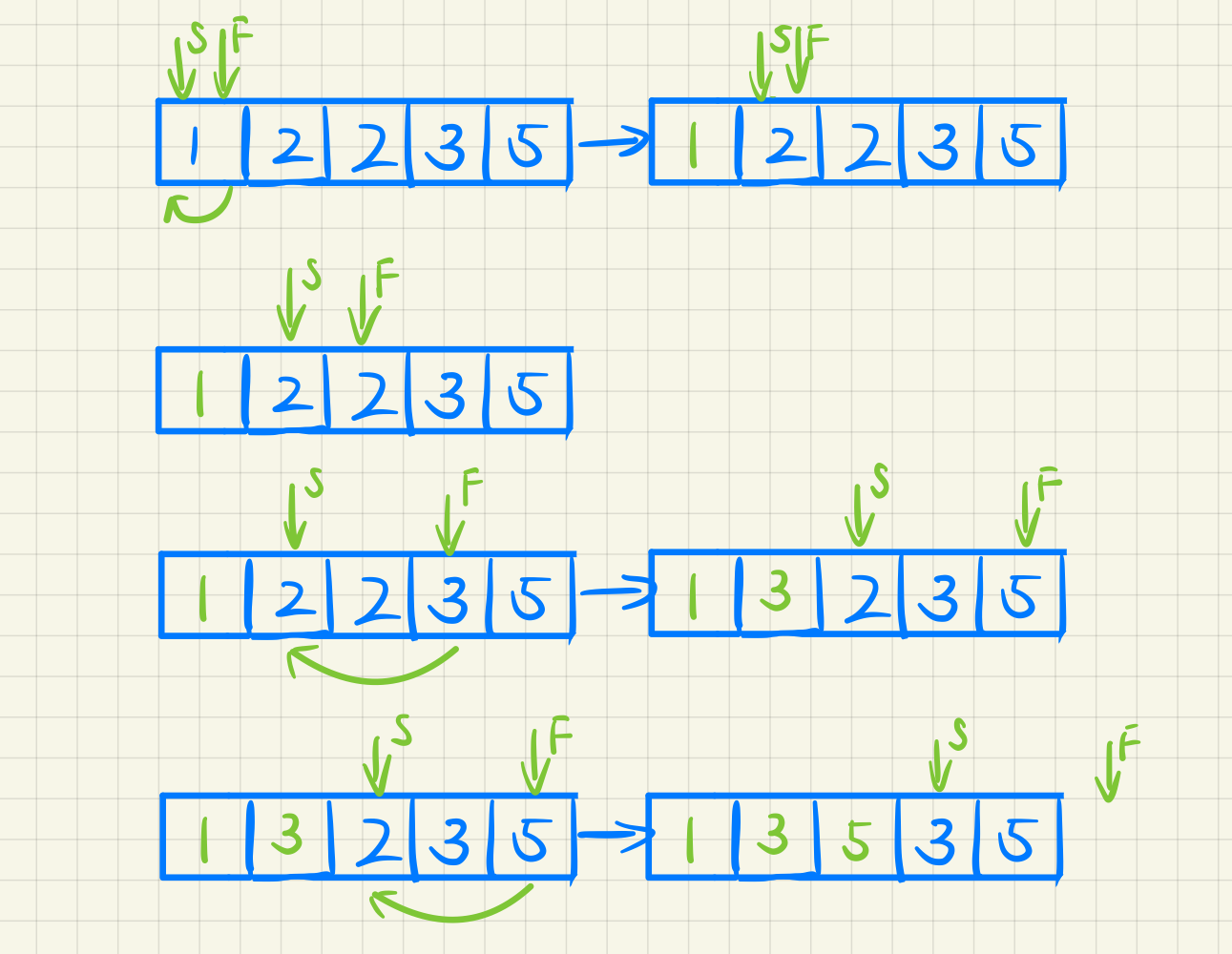
S，F分别代表慢指针和快指针。

例1：删除一个元素2

例2：删除两个元素2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int removeElement(vector<int>& nums, int val)
{
    int slowIndex{0};
  
    // 快指针遍历全部数组
    for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++)
    {
        // 当快指针的值不为待覆盖值时
        // 慢指针值即为快指针的值
        // 且慢指针也向后移动
        if (nums[fastIndex] != val)
            nums[slowIndex++] = nums[fastIndex];
    }
    
    // 慢指针最后所对应的序号即为覆盖删除后的新长度
    return slowIndex;
}

26. 删除有序数组中的重复项（Easy）

使用快慢指针的方法，从序号为 1 的数开始：

  • 如果 num[fast] ≠ num[fast-1]，说明没有重复。
    • 用num[fast] 覆盖num[slow]。
  • 否则说明num[fast]与上一个值重复了，需要删除。
    • slow保持不动，fast指向下一个数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int removeDuplicates(vector<int>& nums)
{
    int length = (int) nums.size();

    if (length == 0) return 0;

    int slow = 1;

    for (int fast = 1; fast < length; fast++)
    {
        if (nums[fast] != nums[fast - 1])
        {
            nums[slow++] = nums[fast];
        }
    }

    return slow;
}

283. 移动零（Easy）

1
2
3
4
5
6
7
8
9
void moveZeroes(vector<int>& nums) {

    int slow = 0;

    for (int fast = 0; fast < nums.size(); fast++)
    {
        if (nums[fast] != 0) swap(nums[slow++], nums[fast]);
    }
}

844. 比较含退格的字符串（Easy）

先用快慢指针法处理字符串中的退格，最后比较两个处理完的字符串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool backspaceCompare(string s, string t)
{
    backspaceString(s);
    backspaceString(t);
    return s == t;
}

void backspaceString(string& s)
{
    int slow = 0;

    for (int fast = 0; fast < s.size(); fast++)
    {
        if (s[fast] != '#')
            s[slow++] = s[fast];
        else if (slow > 0) // 防止第一个字符为 # 时出现数组越界
            slow--;
    }

    s.resize(slow);
}

左右指针

977. 有序数组的平方（Easy）

先平方后排序

  • 时间复杂度：\(O(n+n\log{n})\approx O(n\log{n})\)
  • 空间复杂度（不考虑返回新数组）：\(O(\log{n})\)的栈空间进行排序

双指针

  • 时间复杂度：$ O(n) $
  • 空间复杂度（不考虑返回新数组）：$ O(1) $

因为数组本身是从小到大排序，平方后首尾指针往中间最小值递减。

所以可以使用两个指针分别为left，right ：

新平方数组的从右往左，取两个指针的最大值，然后不断更新左右指针。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
vector<int> sortedSquares(vector<int>& nums)
{
    int index = (int)nums.size();

    vector<int> newNums(index);
    int left = 0, right = index - 1;


    while (left <= right) // 左右两个指针错位，即数组遍历完
    {
        int sqrLeft = nums[left] * nums[left];
        int sqrRight = nums[right] * nums[right];

        if (sqrLeft > sqrRight)
        {
            newNums[--index] = sqrLeft;
            left++;
        }
        else
        {
            newNums[--index] = sqrRight;
            right--;
        }
    }

    return newNums;
}

其他

31. 下一个排列

LeetCode题解 > 数组
#算法题解
双指针
http://blog.ashechol.top/posts/50cab45.html
作者
Ashechol
发布于
2023年1月29日
许可协议