透视矫正插值

三角形经过透视投影变换后，求出的重心坐标系数会不适用于原本三维空间中的三角形，从而导致了直接使用线性的重心坐标插值得不到正确的结果。而透视矫正插值（perspective-correct interpolation）正是为了解决这个问题。

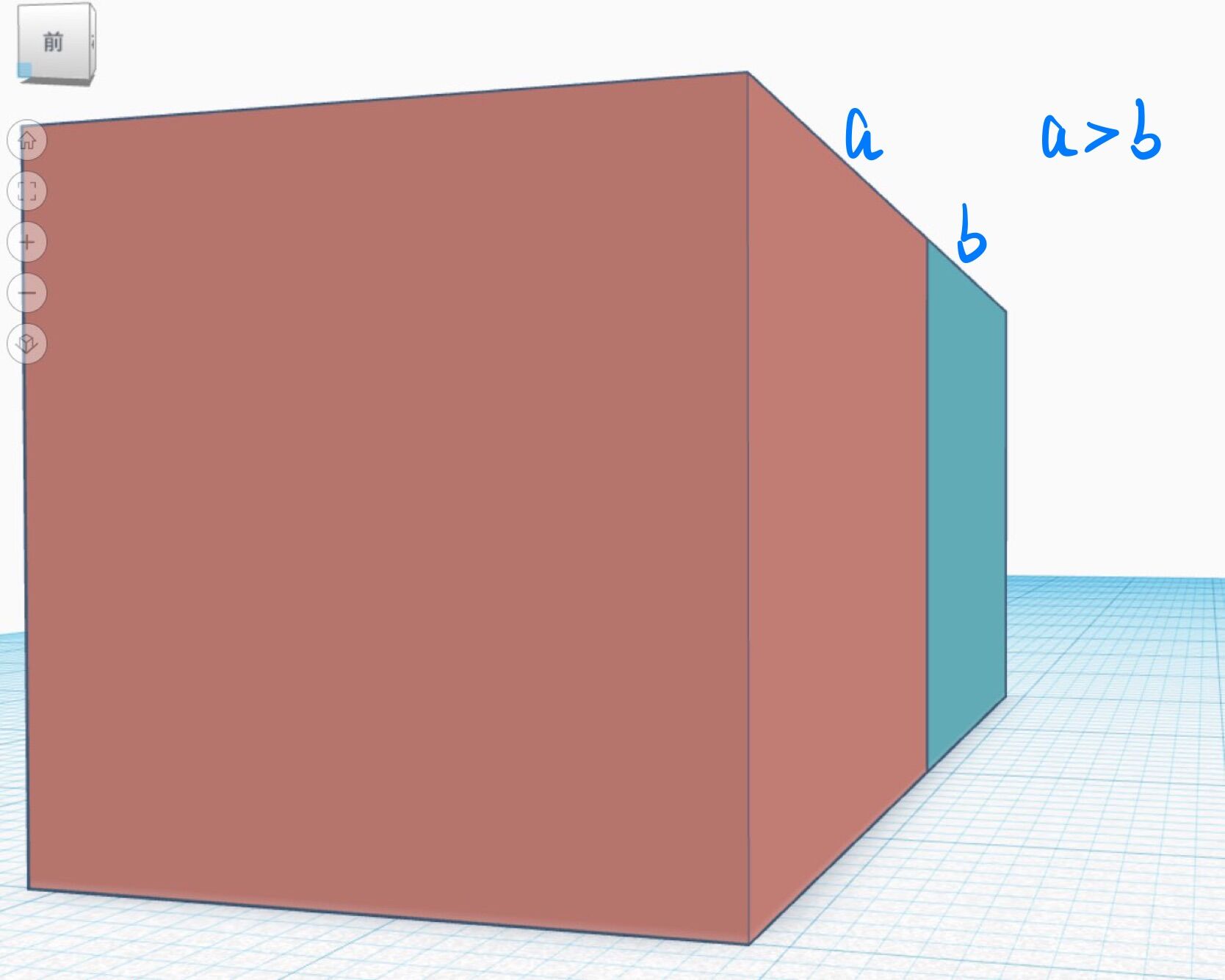
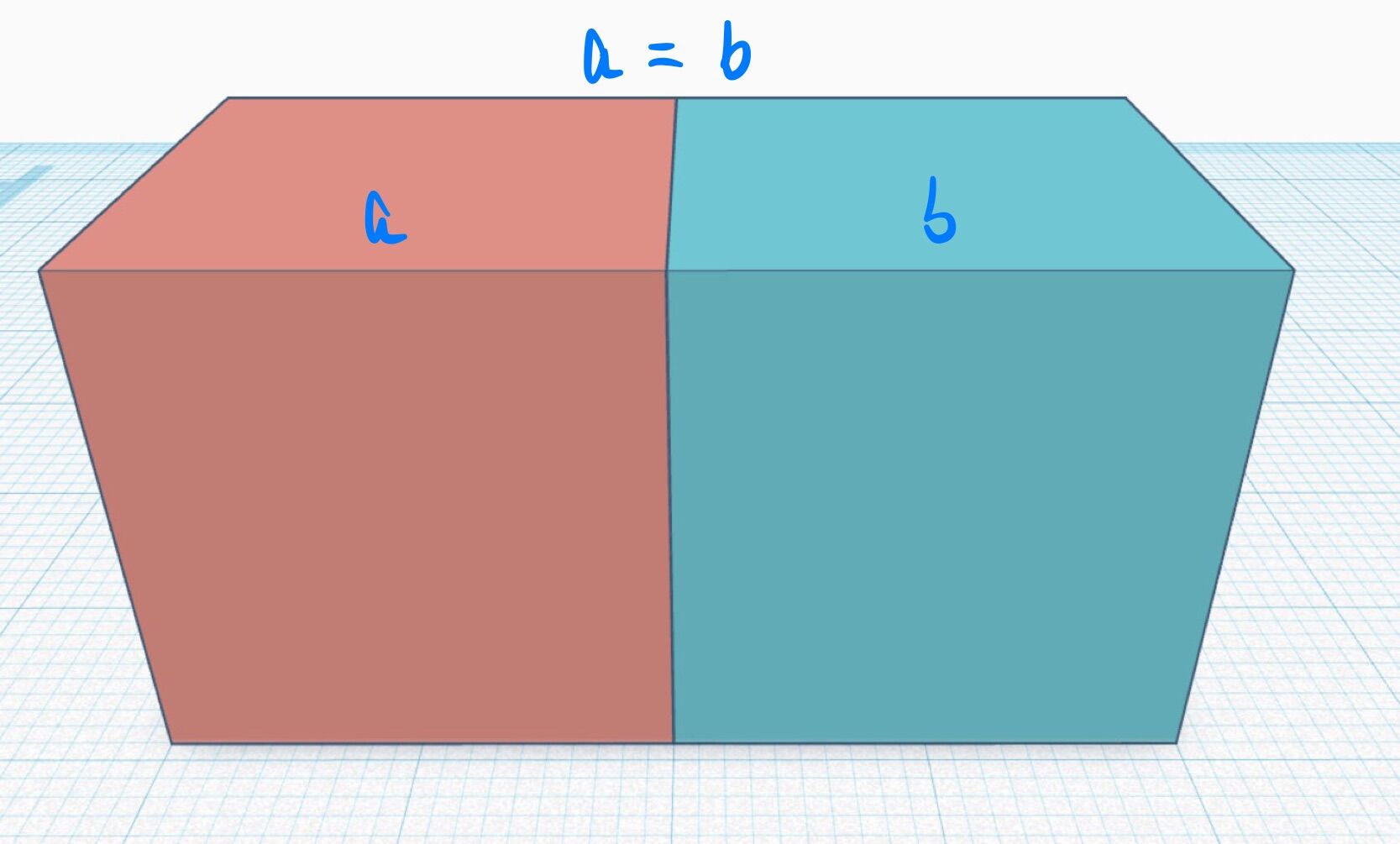
上图可以看出，在透视投影下 \(a>b\) ，而实际上，\(a, b\) 分别是两个同样大小正方形的边长。

如果我们把正方形的面切割成三角形，就可以看出，透视后的三角形和实际的三角形并不相同。自然投影前的重心坐标参数应用于投影后的不会表示相同的点。

在推导透视投影矩阵的时候，我们知道其实透视投影后的一个点的坐标 \(x_p,y_p,z_p\) 与实际三维空间坐标 \(x,y,z\) 关系如下 \[ \begin{align} x_p&=\frac{nx}{z}\\ y_p&=\frac{ny}{z}\\ z_p&=\frac{(n+f)z-nf}{z} \end{align} \] 这样他们从原来的线性关系变成了非线性关系。自然在线性关系下的重心坐标系数也不实用与经过了非线性变换的三角形了，反之亦然。而我们进行重心插值想要的到的是在线性关系下的插值结果，比如，纹理 uv 的插值，颜色的插值等。所以需要一个从非线性的插值结果转换到对应的线性插值结果的方法。

思路

投影变换后的直接线性重心坐标插值如下 \[ f=\alpha f_0+\beta f_1+\gamma f_2\ \ (错误的) \] 其中三个重心坐标系数 \(\alpha,\beta,\gamma\) 是基于投影变换后的三角形的顶点得出。顶点的属性 \(f_0,f_1,f_2\) 是变换前三角形的顶点表示的属性，那么我们这样做插值出来的 \(f\) 是不对的。

我们可以把投影变换后的空间看做一个与 \(1/z\) 相关的非线性空间。那么我们只需要对三个顶点属性做一次非线性变换，然后用基于 \(1/z\) 重心坐标系数便能够线性插值出一个基于 \(1/z\) 空间的属性 \(f_{1/z}\) \[ f_{1/z}=\alpha\frac{f_0}{z_0}+\beta\frac{f_1}{z_1}+\gamma\frac{f_2}{z_2} \] 我们可以把这个线性插值写成向量点积形式 \[ f_{1/z}= \begin{pmatrix} \alpha&\beta&\gamma \end{pmatrix} \begin{pmatrix} f_0/z_0\\ f_1/z_1\\ f_2/z_2 \end{pmatrix} \] 而 \(1/z\) 空间的属性向量的单位向量为 \[ \begin{pmatrix} \frac{1}{z_0}\\ \frac{1}{z_1}\\ \frac{1}{z_2} \end{pmatrix} \] 为了得到正确的插值 \(f\) ，接下来我们对 \(f_{1/z}\) 乘以一个基于 \(1/z\) 空间单位向量线性插值后的倒数 \(r\) 就可以得到了。 \[ f=f_{1/z}r \]

\[ r=\frac{1}{\alpha\frac{1}{z_0}+\beta\frac{1}{z_1}+\gamma\frac{1}{z_2}} \]

最后透视矫正插值公式表示为 \[ f=f_{1/z}r=\frac{\alpha\frac{f_0}{z_0}+\beta\frac{f_1}{z_1}+\gamma\frac{f_2}{z_2}}{\alpha\frac{1}{z_0}+\beta\frac{1}{z_1}+\gamma\frac{1}{z_2}} \]

参考资料

https://www.youtube.com/watch?v=F5X6S35SW2s

https://www.youtube.com/watch?v=1Dv2-cLAJXw