Games101 作业2：光栅化

作业 2

在作业 2，我们要在作业 1 实现的投影矩阵基础上，对两个三角形进行光栅化，且要求光栅化结果要正确表示两个三角形的前后关系。提高任务为实现 MSAA 算法对生成的三角形进行抗锯齿。下面从每个任务点来进行总结。

1. 基本的光栅化

1.1 包围盒

我们首先要确定三角形的包围盒（bounding box）。代码如下：

1
2
3
4
5
// Find out the bounding box of current triangle.
int xMin = floor(std::min(v[0].x(), std::min(v[1].x(), v[2].x())));
int xMax = ceil(std::max(v[0].x(), std::max(v[1].x(), v[2].x())));
int yMin = floor(std::min(v[0].y(), std::min(v[1].y(), v[2].y())));
int yMax = ceil(std::max(v[0].y(), std::max(v[1].y(), v[2].y())));

这里定义整型的原因是为了让我们在 for 循环时将 x，y 作为循环的索引，比如（i, j）。个人认为，这其实算是一种编程规范。如果我们直接使用浮点型， clang-tidy 会提醒 Clang-Tidy: Loop induction expression should not have floating-point type ，即浮点型不适合作为循环的索引值。

后面需要采样点时我们只需转型到浮点然后 x, y 分量各加上对应的变量即可，如像素中点（x + 0.5, y + 0.5）。

1.2 光栅化循环

没有进行 MSAA 的光栅化实际上就是一个二层循环，大体如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
for (int i = xMin; i < xMax; i++)
{
    auto x = static_cast<float>(i);
    for (int j = yMin; j < yMax; j++)
    {
        auto y = static_cast<float>(j);

        // 采样点是否在三角形内
        if (insideTriangle(x + 0.5f, y + 0.5f, t.v))
        {
            // 以下对采样点的 z 轴进行插值
            auto [alpha, beta, gamma] = computeBarycentric2D(x + 0.5f, y + 0.5f, t.v);
            float w_reciprocal = 1.0f / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
            float z_interpolated =
                alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
            z_interpolated *= w_reciprocal;
			
            // z-buffer算法
            if (z_interpolated < depth_buf[get_index(i, j)])
            {
                set_pixel(Vector3f(x, y, 0), t.getColor());
                depth_buf[get_index(i, j)] = z_interpolated;
            }
        }
    }
}

下面从上往下分析。

1.2.1 采样点是否在三角形

这里用到一个 insideTriangle 函数，其定义为

1
2
3
4
5
6
static bool insideTriangle(float x, float y, const Vector3f* _v)
{
    auto [alpha, beta, gamma] = computeBarycentric2D(x, y, _v);

    return alpha > 0 && beta > 0 && gamma > 0;
}

这里用的方法是重心坐标系判定法 ，其三个坐标系参数由函数 computeBarycentric2D 返回的一个浮点型的三元组（tuple）。

代码中元组的用法是 C17 标准引入的新用法

由于我们已经知道 \(\alpha+\beta+\gamma=1\) 且 三个参数都小于 1 时说明点在三角形内。而平面上所有点都满足第一个条件，所以当点在外面时，一定有参数的值小于 0，所以代码这里直接用三个参数都大于 0 判断点在三角形内。

1.2.2 采样点 z 坐标的插值

这里插值使用的是经过 透视矫正 后的 重心坐标 插值。其公式为 \[ f=\frac{\alpha\frac{f_0}{z_0}+\beta\frac{f_1}{z_1}+\gamma\frac{f_2}{z_2}}{\alpha\frac{1}{z_0}+\beta\frac{1}{z_1}+\gamma\frac{1}{z_2}} \] 这里的 z 是指投影变换前的初始顶点 z 坐标。

1
2
3
4
5
6
// 以下对采样点的 z 轴进行插值
auto [alpha, beta, gamma] = computeBarycentric2D(x + 0.5f, y + 0.5f, t.v);
float w_reciprocal = 1.0f / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated =
    alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;

可以看到代码框架给的公式和上述公式大同小异，除了被除数用的齐次坐标下的 w 值。这是因为，此时的 z 值已经是被投影变换后的了，而齐次坐标下 w 经过投影变换后存储的值是初始的 z 值（详见 投影变换 )。

需要注意的是，作业二的代码框架中，这里的 w 是在 rasterize_triangle 函数第一行，通过 toVector4 函数，转换为 Vector4f 的顶点的 w，其值为 1 。

所以此处插值没有达到透视矫正的效果只是一般的重心坐标线性插值。不过对于作业二的结果来说没有影响罢了。在作业三中，这里的错误已修改。

1.2.3 z-buffer 算法

得到了插值后的采样点的深度值后，接下来就是通过深度测试来判断该采样点是否绘制其对应的像素了。

1
2
3
4
5
6
// z-buffer算法
if (z_interpolated < depth_buf[get_index(i, j)])
{
    set_pixel(Vector3f(x, y, 0), t.getColor());
    depth_buf[get_index(i, j)] = z_interpolated;
}

z-buffer 算法本身简单易懂。这里需要注意的是远近的判断问题。

Games101 课程中，我们认为摄像头是在原点看向 -Z。所以在作业一的投影变换函数中，我们队输入为正的近远平面深度取了负。

但是在作业二中，我们对深度的判断采用了深度的正值。而且作业框架视口变换部分用了以下代码，将深度范围从 [-1, 1] 变为了 [0.1, 50]。

1
vert.z() = vert.z() * f1 + f2;

这里用的 z 应该是正值，而我们 z 为负，所以少了一个负号。最后会导致深度值转换后两个三角形前后交换。应改为

1
vert.z() = -vert.z() * f1 + f2;

1.3 结果

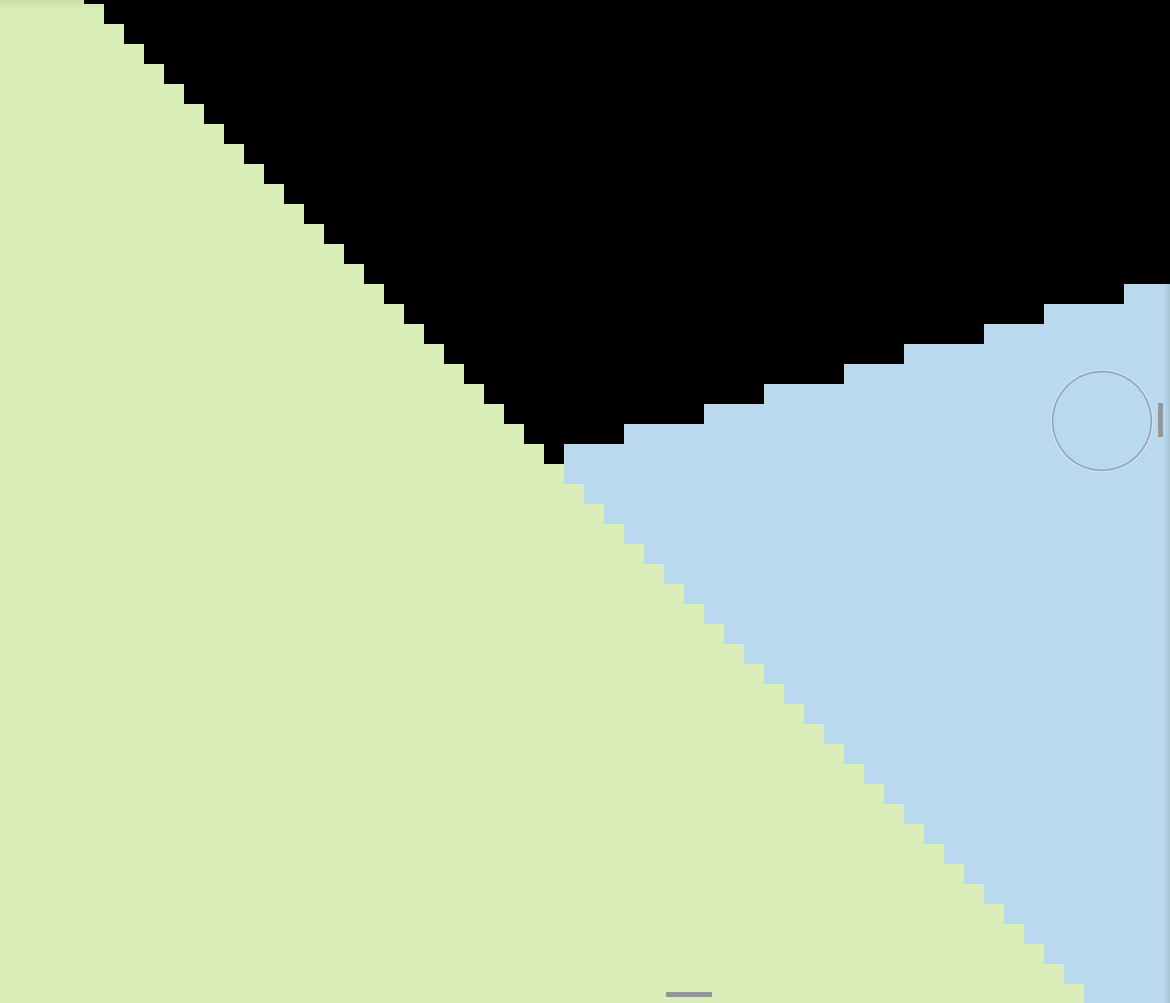
做完上述步骤，可以得到没有开启抗锯齿的图像了。如下所示

可以看到蓝色三角形有较为明显的锯齿。放大后如图所示

2. MSAA 抗锯齿

2.1 有瑕疵（黑/灰/暗边）的实现方案

按照 Games 101 中 MSAA 最直接的思路来实现。

MSAA 的思路可以参考 笔记 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// Anti-aliasing on
int cnt = insideTriangle(x + 0.25f, y + 0.25f, t.v) +
          insideTriangle(x + 0.25f, y + 0.75f, t.v) +
          insideTriangle(x + 0.75f, y + 0.25f, t.v) +
          insideTriangle(x + 0.75f, y + 0.75f, t.v);

auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
float w_reciprocal = 1.0f / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated =
    alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;

if (cnt > 0 && z_interpolated < depth_buf[get_index(i, j)])
{
    depth_buf[get_index(i, j)] = z_interpolated;
    set_pixel(Vector3f(x, y, 0), cnt / 4.0f * t.getColor());
}

首先我们直接对每个每个子采样点（subsample point）进行是否在三角形内的判断，存储在整型变量 cnt 中

1
2
3
4
int cnt = insideTriangle(x + 0.25f, y + 0.25f, t.v) +
          insideTriangle(x + 0.25f, y + 0.75f, t.v) +
          insideTriangle(x + 0.75f, y + 0.25f, t.v) +
          insideTriangle(x + 0.75f, y + 0.75f, t.v);

然后还是按照正常流程求采样点（注意，不是子采样点）的用于深度测试的深度值

之后便是按照最基础思路，如果我们的 cnt 大于 0 就说明有子采样点在三角形中，所以父采样点应该进行深度测试。

1
2
3
4
5
6
7
8
if (cnt > 0 && z_interpolated < depth_buf[get_index(i, j)])
{
    depth_buf[get_index(i, j)] = z_interpolated;
    
    // 注意 cnt / 4 涉及到转型问题，cnt 和 4 都为整型最后得到的值会向下取整，即永远为 0
    // 所以我们要用 cnt / 4.0f
    set_pixel(Vector3f(x, y, 0), cnt / 4.0f * t.getColor());
}

在 set_pixel 函数中，我们对采样点原本的颜色 t.getColor() 乘上了在三角形内子采样点的百分比 cnt/4，这样就完成了 MSAA 最基本的思路。

最后结果如图所示

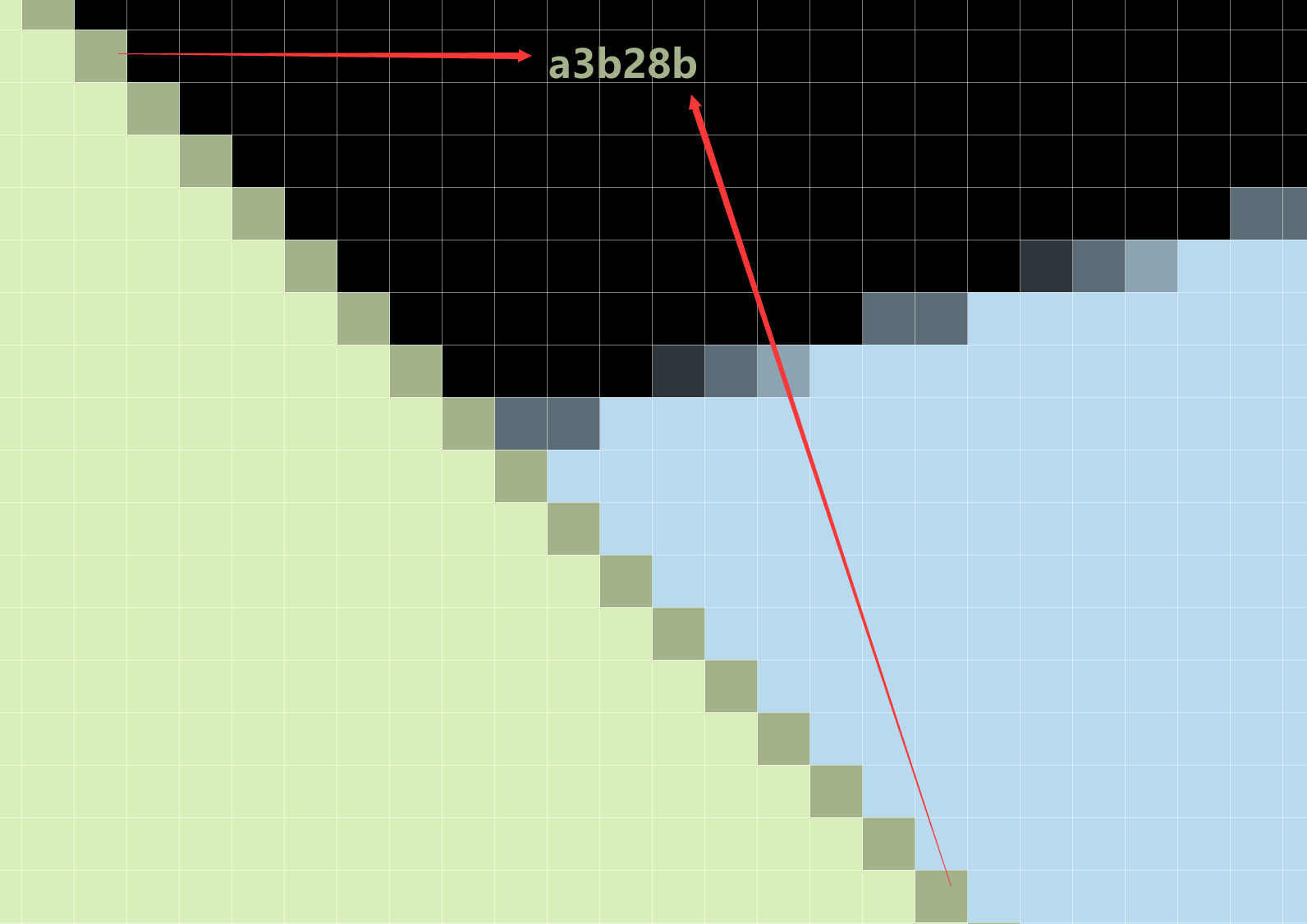
仔细看可以发现，两个三角形的交界处有一条灰边（有的人可能是颜色更深的黑边）。放大仔细观察

使用采色器对于三角形于背景（黑），和蓝色三角形，两者边界像素的采色结果其实是一样的（a3b28b）。由于背景不同，人眼观察会产生色彩误差，让我们认为和蓝色三角形的边界变暗了，即暗边。

在学习 反走样/抗锯齿 时，我们先了解了模糊后采样来抗锯齿的方法。而模糊的操作实际上是对，每个像素何其其邻近像素颜色的加权平均后的平滑值。

所以我们在 MSAA 时不能只考虑 在三角形内子采样点 的颜色，还要考虑三角形外的颜色。在上述的代码中，我们的操作实际上是把三角形外的子采样点全部当做黑色，即 rgb(0, 0, 0) 来处理。这样操作就没有考虑到与蓝色三角形的颜色了。

2.2 MSAA 真正的实现方案

2.2.1 子采样点的颜色缓冲和深度缓冲

既然我们知道了要将所有子采样点的颜色考虑进去然后求平均，那么首先我们需要定义一个用于存储子采样点颜色的 subsample_color_buf 。既然我们要对子采样点的颜色进行判断，那自然也会涉及到前后覆盖的问题，所以我们也要同时维护一个 subsample_depth_buf 。

在代码框架中，我们的深度缓冲变量的定义是存储在 rasterizer.hpp 的 rasterizer 类中，我们的也将新的变量定义在其中

1
2
3
4
5
6
7
8
9
10
11
// rasterizer.hpp
class rasterizer
{
    ...
        
    std::vector<float> depth_buf;
    std::vector<float> subsample_depth_buf;
    std::vector<Eigen::Vector3f> subsample_color_buf;
    
    ...
}；

我们将缓冲定义为一个一维数组，其大小为深度缓冲的 4 倍，即 700x700x4 。在代码框架中 rasterizer 类的构造函数中，我们对数组进行了 resize

这里的 vector 是 c++ stl 容器之一，为了避免歧义，我们还是将其叫做数组。

1
2
3
4
5
6
7
rst::rasterizer::rasterizer(int w, int h) : width(w), height(h)
{
    frame_buf.resize(w * h);
    depth_buf.resize(w * h);
    subsample_color_buf.resize(w * h * 4);
    subsample_depth_buf.resize(w * h * 4);
}

因为是一维数组，我们也要实现一个 get_subsample_index 用于将三维的索引转换为一维。

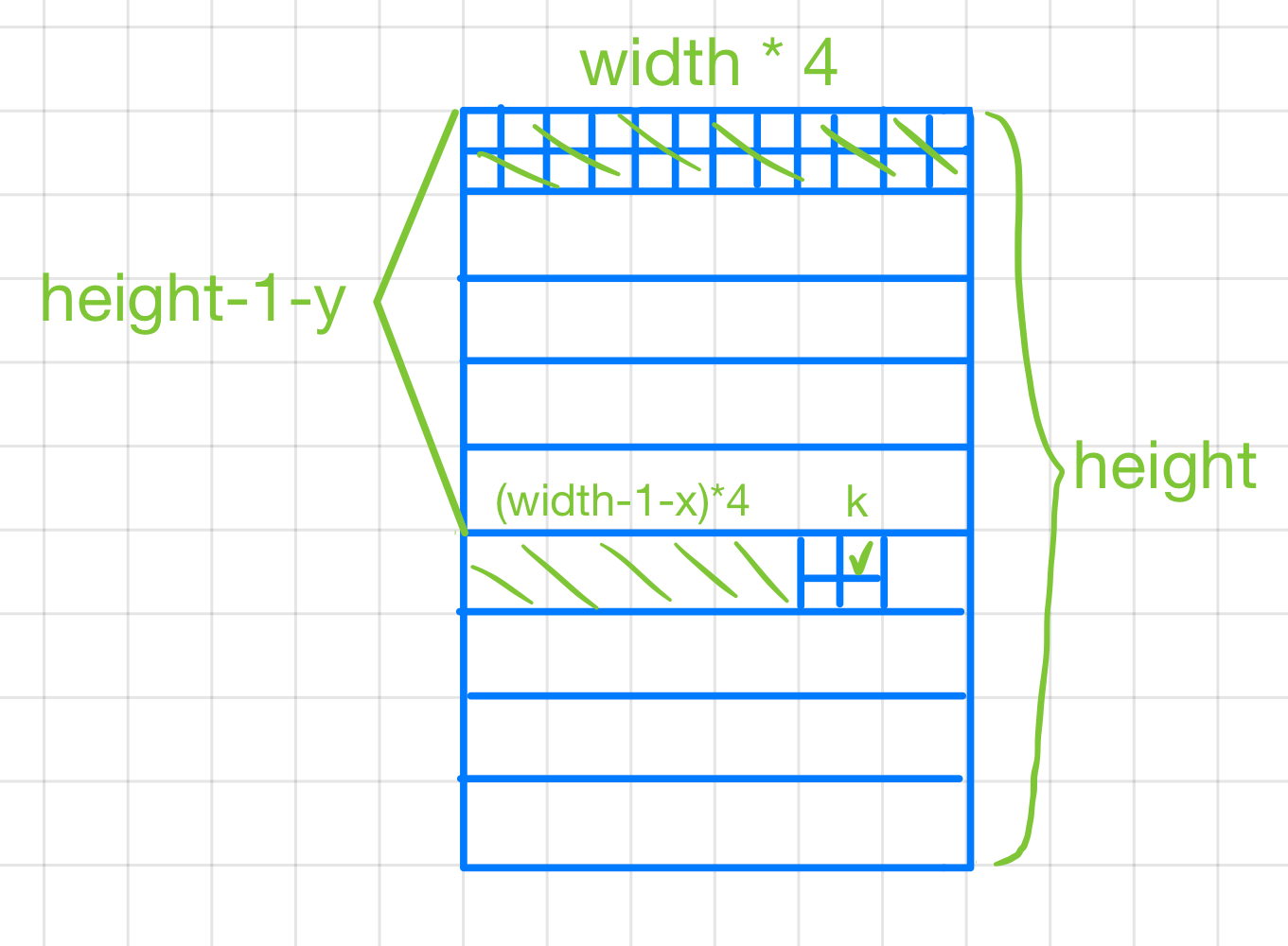
1
2
3
4
int rst::rasterizer::get_subsample_index(int x, int y, int k) const
{
    return (height - 1- y) * width * 4 + (width - 1 - x) * 4 + k;
}

这个公式的计算如下图所示：

我们还需要一个函数 get_sample_color 用于从子采样点的颜色缓冲计算出对应父采样点的颜色。如下所示

1
2
3
4
5
6
7
8
9
Vector3f rst::rasterizer::get_sample_color(int x, int y) const
{
    int index = get_subsample_index(x, y, 0);
    Vector3f sum{0, 0, 0};
    for (int i = 0; i < 4; i++)
        sum += subsample_color_buf[index + i];

    return sum / 4.0f;
}

在这个函数中，我们计算了四个子采样点的颜色合，然后对其求平均后返回。

2.2.2 修改 MSAA 的实现部分

修改后如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Vector2f x4[4] = {{0.25, 0.25},
                  {0.25, 0.75},
                  {0.75, 0.25},
                  {0.75, 0.75}};
bool depth_test = false;
for (int k = 0; k < 4; k++)
{
    if (!insideTriangle(x + x4[k].x(), y + x4[k].y(), t.v))
        continue;

    auto [alpha, beta, gamma] = computeBarycentric2D(x + x4[k].x(), y + x4[k].y(), t.v);
    float w_reciprocal = 1.0f / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
    float z_interpolated =
        alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
    z_interpolated *= w_reciprocal;

    int index = get_subsample_index(i, j, k);
    if (z_interpolated < subsample_depth_buf[index])
    {
        subsample_depth_buf[index] = z_interpolated;
        subsample_color_buf[index] = t.getColor();
        depth_test = true;
    }
}

if (depth_test)
    set_pixel(Vector3f(x, y, 0), get_sample_color(i, j));

为了方便计算，我们在光栅化函数的二重循环中嵌套了对四个子采样点的循环，同时我们将采样点偏移量存入数组中便于使用。此外我们不再使用 cnt 来统计三角形内子采样点的数量，而是用一个布尔变量 depth_test 用来判断是否有子采样点通过深度测试。只要有一个子采样点通过了深度测试，我们就应该更新父采样点对应的像素。

1
2
3
4
5
6
7
8
9
10
Vector2f x4[4] = {{0.25, 0.25},
                  {0.25, 0.75},
                  {0.75, 0.25},
                  {0.75, 0.75}};

bool depth_test = false;
for (int k = 0; k < 4; k++)
{
    ...
}

对 子采样点 的处理和对 采样点 的处理大同小异，依次是三角形内判断，深度的重心坐标插值。唯一不同的是，我们要更新子采样点的深度缓冲和颜色缓冲

1
2
3
4
5
6
7
int index = get_subsample_index(i, j, k);
if (z_interpolated < subsample_depth_buf[index])
{
    subsample_depth_buf[index] = z_interpolated;
    subsample_color_buf[index] = t.getColor();
    depth_test = true;
}

这里我们子采样点的颜色直接取自父采样点。如果我们对子采样点的颜色进行插值，那么开销会变更大，但是最后的抗锯齿效果也会更好。这点也是 SSAA（Super Sampling Anti-aliasing） 与 MSAA 的不同之处。

最后如果有子采样点通过了深度测试，我们更新父采样点对应的像素。

1
2
if (depth_test)
    set_pixel(Vector3f(x, y, 0), get_sample_color(i, j));

这里 set_pixel 函数的颜色参数我们使用子采样点的平均颜色。

2.3 最终效果

最终效果如下

放大后如下所示

相关链接

笔记：计算机图形学笔记(1)：光栅化

完整源码：Github

参考材料

《GAMES101》作业框架问题详解

MSAA和SSAA的详细说明

图形学 > Games101
#图形学 #C++ #光栅化 #抗锯齿
Games101 作业2：光栅化
http://blog.ashechol.top/posts/26626c91.html
作者
Ashechol
发布于
2023年1月13日
许可协议