排序
冒泡排序
O(n^2)
O(n^2)
O(n)
O(1)
是
选择排序
O(n^2)
O(n^2)
O(n^2)
O(1)
否
插入排序
O(n^2)
O(n^2)
O(n)
O(1)
是
希尔排序
取决于间隔序列
取决于间隔序列
取决于间隔序列
O(1)
否
归并排序
O(n log n)
O(n log n)
O(n log n)
O(n)
是
快速排序
O(n^2)
O(n log n)
O(n log n)
O(log n)
否
堆排序
O(n log n)
O(n log n)
O(n log n)
O(1)
否
计数排序
O(n + k)
O(n + k)
O(n + k)
O(k)
是
冒泡排序
1 2 3 4 5 6 7 8 9 10 11 12 void BubbleSort (vector<int >& nums) for (int i = 0 ; i < nums.size (); ++i)for (int j = 1 ; j < nums.size () - i; ++j)if (nums[j-1 ] > nums[j])swap (nums[j-1 ], nums[j]);
选择排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void SelectionSort (vector<int >& nums) for (int i = 0 ; i < nums.size (); ++i)int mi = i;for (int j = i; j < nums.size (); ++j)if (nums[j] < nums[mi])swap (nums[i], nums[mi]);
插入排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void InertionSort (vector<int >& nums) for (int i = 1 ; i < nums.size (); ++i)int j = i;int k = nums[j];while (j > 0 && nums[j-1 ] > k)-1 ];
希尔排序
希尔排序是插入排序的优化版本。因为当一个数组趋向于有序的时候,插入排序的效率会很高。所以希尔排序利用不断变小的间隔,对数组的元素进行分组插入排序,这样每一次间隔都可以得到区域有序的数组。
一般的插入排序就是间隔为 1 时的希尔排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 void ShellSort (vector<int >& nums) int gap = nums.size () / 2 ;while (gap > 0 )for (int i = gap; i < nums.size (); ++i)int j = i;int k = nums[i];while (j > 0 && nums[j-gap] > k)2 ;
如果希尔排序的间隔序列是每次除以 2,也就是缩小为原来的一半,这种情况下称为希尔增量或 Hibbard 增量。
希尔排序在这种增量序列下的时间复杂度为 \(O(n^{1.5})\) 。这是一个相对较好的性能,尤其对于中等大小的数据集来说。
归并排序
通过递归不断划分左右区间,之后合并排序。需要注意的是递归左右的终止条件是 right - left <= 1 或者说 right - left == 1 ,这是因为作为边界传入的mid 并不需要像在二分查找或者快排中那样被排除掉。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 void Merge (vector<int >& nums, int left, int mid, int right) int ln = mid - left, rn = right - mid;vector<int > lNums (ln) , rNums (rn) ;for (int i = left; i < mid; ++i) lNums[i - left] = nums[i];for (int i = mid; i < right; ++i) rNums[i - mid] = nums[i];int l = 0 , r = 0 , i = left;while (l < ln && r < rn)if (lNums[l] <= rNums[r])else while (l < ln) nums[i++] = lNums[l++];while (r < rn) nums[r++] = rNums[r++];void MergeSort (vector<int >& nums, int left, int right) if (right - left == 1 ) return ;int mid = left + ((right - left) >> 1 );MergeSort (nums, left, mid);MergeSort (nums, mid, right);Merge (nums, left, mid, right);
快速排序
Hoare 快排
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void Sort (vector<int >& nums, int bg, int ed) if (bg >= ed) return ;int left = bg + 1 , right = ed - 1 ;while (true )while (left < nums.size () && nums[left] < nums[bg]) ++left;while (right >= 0 && nums[right] > nums[bg]) --right;if (left >= right) break ;swap (nums[left], nums[right]);swap (nums[right], nums[bg]);Sort (nums, bg, right);Sort (nums, right + 1 , ed);
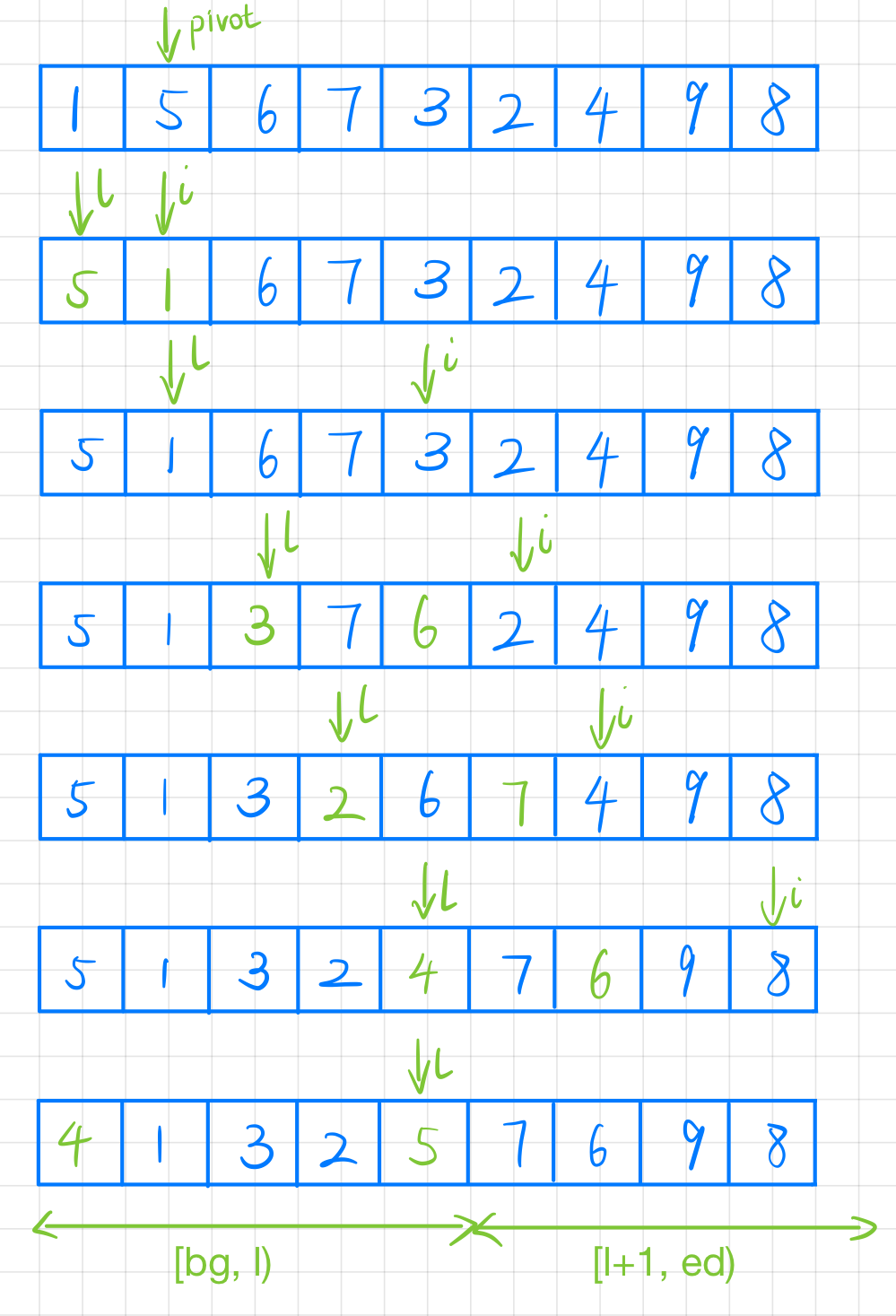
Lomuto 快排
lomuto 的思想主要是探针 i 从左到右遍历,通过更新小于 pivot 的数的最右下标 left 分割数组。这个方法边界判定简单,不容易写错。
基础快排
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 void quickSort (vector<int >& nums, int bg, int ed) if (bg >= ed) return ;int randInd = bg + rand () % (ed - bg);swap (nums[bg], nums[randInd]);int pivot = nums[bg];int l = bg;for (int i = bg + 1 ; i < ed; i++)if (nums[i] < pivot)swap (nums[i], nums[++l]); swap (nums[l], nums[bg]);quickSort (nums, bg, l);quickSort (nums, l+1 , ed);
三路快排
当输入的数组有大量连续重复值时,上面的写法效率很低了。这个时候把待处理的数组分成 小于 pivot ,大于 pivot 和 等于 pivot 三个部分:。
在 left 记录小于部分最右下标的基础上,引入 right 记录大于部分最左小标,这样区间如下所示:
[bg, left)[left, right)[right, ed)
这样分治的时候可以跳过中间重复的相同值,从而提升效率。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 void quickSort (vector<int >& nums, int bg, int ed) if (bg >= ed) return ;int randInd = bg + rand () % (ed - bg);swap (nums[bg], nums[randInd]);int pivot = nums[bg];int l = bg, r = ed;for (int i = bg + 1 ; i < r; )if (nums[i] < pivot)swap (nums[i++], nums[++l]); else if (nums[i] > pivot)swap (nums[i], nums[--r]); else swap (nums[l], nums[bg]);quickSort (nums, bg, l);quickSort (nums, r, ed);
相关题目 :75. 颜色分类
堆排序
堆实际上是有个每个节点都大于子节点的二叉树。
对于顺序存储的数组,要表示二叉树的结点,序号 i 有以下性质(根节点为 0 时):
左子节点为 i * 2 + 1
右子节点为 i * 2 + 2
子节点的下标为 i 则他的父节点是 (i - 1) / 2
堆排序涉及到一个堆化(heapify)的过程。该过程的步骤是:
比较当前节点和它的左右子节点,找出最大的值;
交换当前节点和最大值的节点;
对被交换了的子节点重复进行以上操作(递归);
利用堆的特性可以对堆表示的数组进行排序,步骤如下:
自底向上地建堆:从最后一个叶子节点的父节点,即下表为 ((n - 1) - 1) / 2 的元素开始堆化;
堆排序(这里默认是大顶堆,从小到大排序):
将堆顶的元素和数组最后一个元素交换;
重新堆化剩下没确定位置的元素;
重复以上两步直到全部元素位置确定;
为什么自底向上建堆而不是自顶向下?在堆元素很多的情况,自顶向下元素的交换次数比自底向上多,从而效率更低。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 void Heapify (vector<int >& nums, int n, int root) int left = root * 2 + 1 ;int right = root * 2 + 2 ;int largest = root;if (left < n && nums[left] > nums[largest])if (right < n && nums[right] > nums[largest])if (largest != root)swap (nums[root], nums[largest]);Heapify (nums, n, largest);void HeapSort (vector<int >& nums) for (int i = nums.size () / 2 - 1 ; i >= 0 ; --i)Heapify (nums, nums.size (), i);for (int i = 1 ; i < nums.size (); ++i)swap (nums[0 ], nums[nums.size () - i]);Heapify (nums, nums.size () - i, 0 );
计数排序
该方法仅适用于整数且最大最小值差距不是很大的排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void CountingSort (vector<int >& nums) int ma = nums[0 ], mi = nums[0 ];for (int & num: nums)max (num, ma);min (num, mi);vector<int > count (ma - mi + 1 , 0 ) ;for (int & num: nums)for (int i = 0 , j = 0 ; i < ma - mi + 1 ; ++i)while (count[i]--)
左闭右开下,左右下标的条件
当仅对数组进行划分,mid 仅作为范围边界时,区间被划分为 [left, mid) 和 [mid, right),则遍历条件是 right - left > 1 。
当每次都要和 mid 进行判断并排除 mid(区间范围都被减了 1),范围变成了 [left, mid) 和 [mid+1, right),则条件是 right - left > 0 。