KMP算法

匹配算法

KMP算法的目标是，避免重复匹配从而减小时间复杂度。如：

• 字符串：aabaabaafbaa

• 模式串：aabaaf

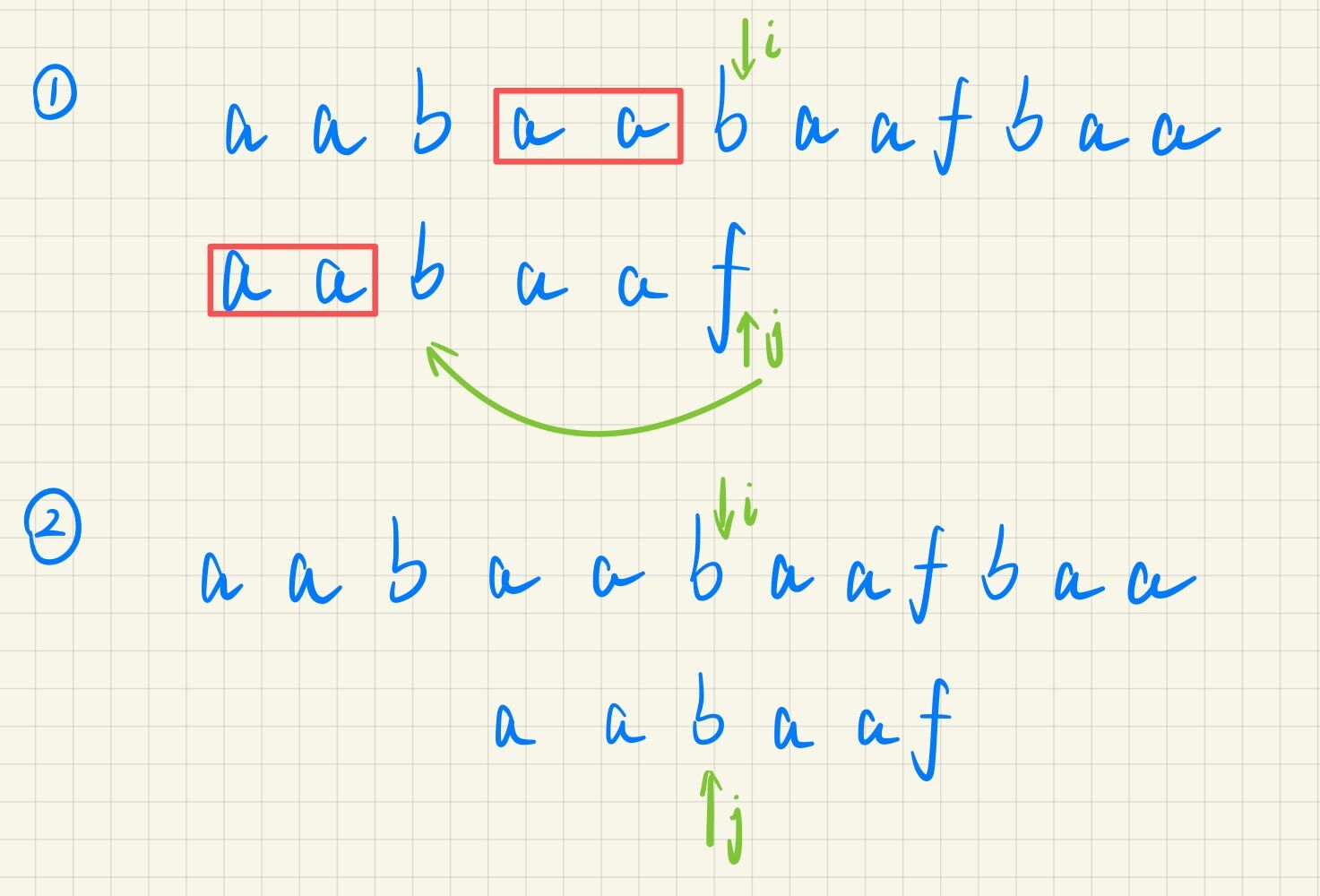
按照暴力模拟的思路。遍历到第六个字符b时，与模式串的第六个字符f不匹配，则需要从第二个字符a重新开始匹配。

而KMP算法可以找出之前已经匹配过的子串aa 从而字符串可以继续往后遍历不用回退，只用回退模式串的到第三个字符b。

前缀表

KMP匹配的方法是基于一个叫做前缀表的数组（有时候也被称为prev数组或next数组）。通过前缀表，可以快速得到模式串当前字符退回的位置。

例如aabaaf的前缀表为：[0, 1, 0, 1, 2, 0]。为了方便代码的实现，一般会往左移 [-1, 0, 1, 0, 1, 2]。

使用两个指针 pre 和 suf ：

• pre = -1

• suf = 0

str[pre] 是前缀的最后一个字符，str[suf] 是后缀的最后一个字符

如果 str[pre]==str[suf] 则两者继续向后比较，next[suf] 记录当前 pre 的位置。

vector<int> getNext(string& pattern)
{
    vector<int> next(1, 0);

    int i = 1, prefixLen = 0;
    while (i < pattern.length())
    {
        if (pattern[prefixLen] == pattern[i])
        {
            next.emplace_back(++prefixLen);
            ++i;
        }
        else if (prefixLen == 0)
        {
            next.emplace_back(0);
            ++i;
        }
        else
            prefixLen = next[prefixLen - 1];
    }

    return next;
}
int patternMatch(string& str, string& pattern)
{
    auto next = getNext(pattern);

    for (int i = 0, j = 0; i < str.length();)
    {
        if (str[i] == pattern[j])
        {
            ++i;
            ++j;
        }
        else if (j > 0)
            j = next[j-1];
        else
            ++i;

        if (j == pattern.length())
            return i - j;
    }

    return -1;
}