计算机图形学笔记(1)：变换

变换（Transformation）

1 2D 变换

2D变换矩阵（齐次坐标系）如下：

• 缩放：

  \[ \textbf{S}(s_x,s_y)=\begin{bmatrix}s_x&0&0\\0&s_y&0\\0&0&1\end{bmatrix}\\ \]

• 切变：

  \[ \textbf{H}(a_x,a_y)=\begin{bmatrix}1&a_x&0\\a_y&1&0\\0&0&1\end{bmatrix}\\ \]

• 旋转：

  \[ \textbf{R}(\alpha)=\begin{bmatrix}\cos\alpha&- \ sin\alpha&0\\\sin\alpha&\cos\alpha&0\\0&0&1\end{bmatrix}\\ \]

• 平移：

  \[ \textbf{T}(t_x,t_y)=\begin{bmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{bmatrix} \]

1.1 缩放（scale）

对于一个 2D 图像的点 \((x,y)^T\) 相对于原点按照 \(X,Y\) 轴的缩放，可以表示为以下公式：

\[ \begin{align} x'=s_xx\\ y'=s_yy \end{align} \]

转化为缩放矩阵乘向量的形式可表示为：

\[ \begin{bmatrix} x'\\ y' \end{bmatrix}= \begin{bmatrix} s_x&0\\ 0&s_y \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} \]

如果 \(x'=-x\) ，图像水平对称；\(y'=-y\) 则垂直对称。

1.2 切变（shear）

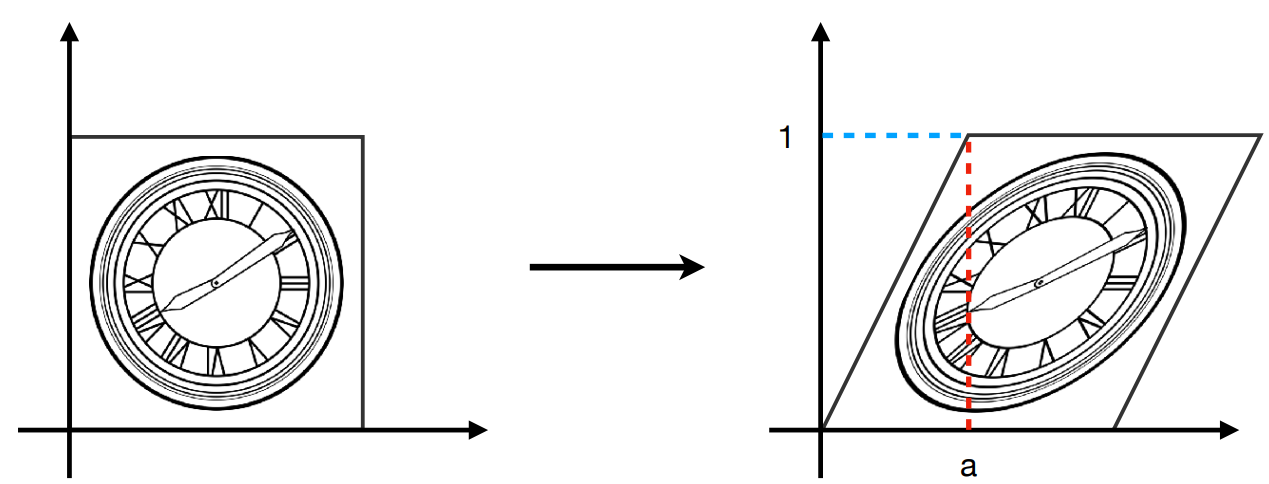
对于一个 2D 图像的点 \((x,y)^T\) 相对于原点按照 \(X\) 或 \(Y\) 轴的切变，可以表示为以下公式：

\[ \begin{align} x'=x+a_xy\\ y'=a_yx+y \end{align} \]

转化为缩放矩阵乘向量的形式可表示为：

\[ \begin{bmatrix} x'\\ y' \end{bmatrix}= \begin{bmatrix} 1&a_x\\ a_y&1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} \]

1.3 旋转（rotation）

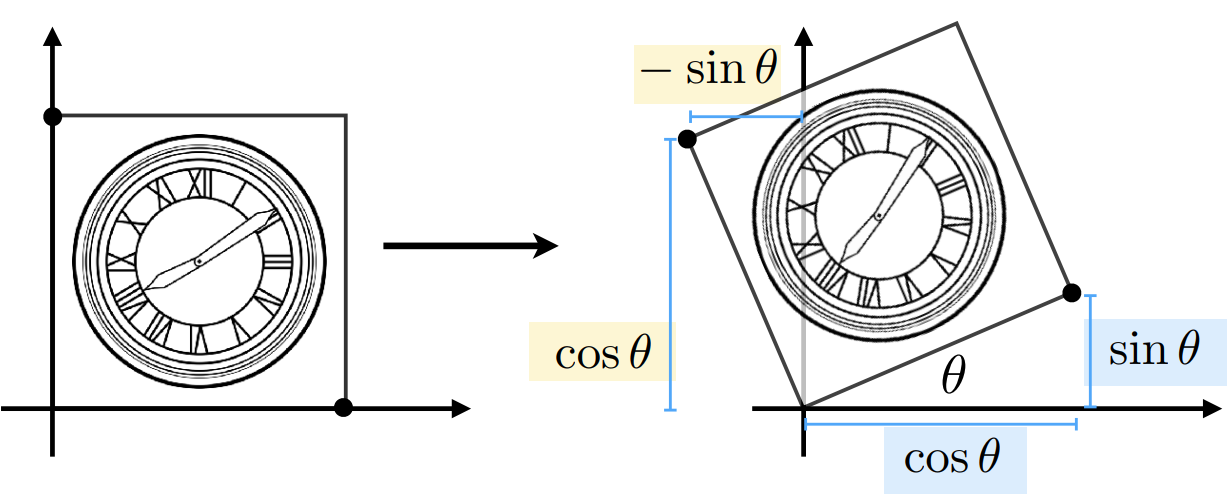
对于一个 2D 图像的点 \((x,y)^T\) 相对于原点逆时针旋转（CCW， counterclockwise），设旋转矩阵 \(\mathbf R_\theta\)：

\[ \mathbf R_\theta= \begin{bmatrix} a&b\\ c&d \end{bmatrix} \]

则 \((x',y')\)表示为：

\[ \begin{align} \:\begin{bmatrix} x'\\ y' \end{bmatrix}&= \begin{bmatrix} a&b\\ c&d \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix}\\ x'&=ax+by\\ y'&=cx+dy \end{align} \]

带入上图中特殊点 \((1,0)^T,(0,1)^T\) 可得：

\[ \begin{align} \cos\theta=a\\ \sin\theta=c\\ -\sin\theta=b\\ \cos\theta=d \end{align} \]

所以得旋转矩阵 \(\mathbf{R}_\theta\) ：

\[ \mathbf R_\theta= \begin{bmatrix} \cos\theta&-\sin\theta\\ \sin\theta&\cos\theta \end{bmatrix} \]

此外可知 \(\boldsymbol R_{-\theta}\) 为: \[ \mathbf R_{-\theta}= \begin{bmatrix} \cos\theta&\sin\theta\\ -\sin\theta&\cos\theta \end{bmatrix}=\mathbf R_\theta^T=\mathbf R_\theta^{-1} \] 所以旋转矩阵是正交矩阵。

1.4 平移（translation）

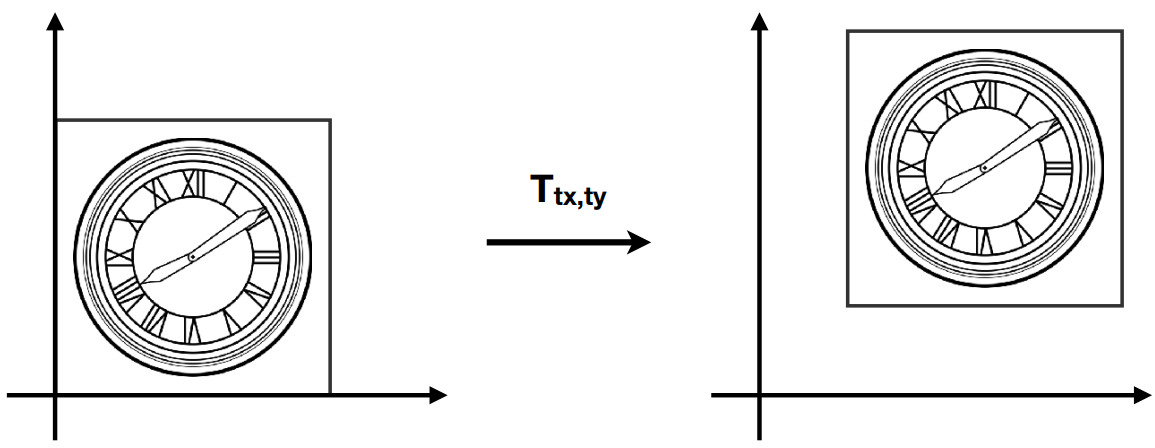
对于一个 2D 图像的点 \((x,y)^T\) 相对于原点进行位移可以通过 仿射变换（仿射映射）表示为：

\[ \begin{bmatrix}x'\\y'\end{bmatrix}= \begin{bmatrix}a&b\\c&d\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}+ \begin{bmatrix}t_x\\t_y\end{bmatrix} \]

可以发现，仅用一个二维矩阵无法表示平移，因此引入 齐次坐标，用三阶矩阵来表示变换矩阵，定义如下：

• 对于点 \((x,y)^T\) ：
  • 添加一个维度表示为 \((x,y,1)^T\)
  • 此外在齐次坐标中 \((x,y,w)^T\) 表示一个 2D 点 \((x/w,y/w,1)\) (\(w\neq0\))
• 对于向量 \((x,y)^T\)
  • 添加一个维度表示为 \((x,y,0)^T\) (向量没有位置属性，所以第三个维度值为0)

所以用齐次坐标位移可以表示为：

\[ \:\begin{bmatrix}x'\\y'\\1\end{bmatrix}= \begin{bmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{bmatrix} \begin{bmatrix}x\\y\\1\end{bmatrix}= \begin{bmatrix}x+t_x\\y+t_y\\1\end{bmatrix} \]

同理，齐次坐标下的缩放、切变和旋转可以表示为本节开头所给出的矩阵。

此外，经过以上定义，齐次坐标中的向量和点仍然满足二维坐标中的性质：

• 向量 + 向量 = 向量
• 点 - 点 = 向量
• 点 + 向量 = 点 （点沿着向量的方向移动）

此外还具有一个特殊性质：

• 点 + 点 = 两点之间中点

2 逆变换和复合变换

2.1 逆变换

由矩阵本身的性质可知：矩阵 \(\textbf{M}^{-1}\) 是 矩阵 \(\textbf{M}\) 所产生变换的逆变换。

2.2 复合变换

当缩放、切变、旋转和位移这些变换组合在一起时，形成了图形的复合变换。

比如：将一个 2D 图形旋转 \(45^\circ\) 然后沿着 \(X\) 轴正方向移动1个单位距离

需要注意的是，在复合变换中，交换不同变换的顺序是会产生截然不同的结果的，这一点也与矩阵乘法性质相吻合。

如下等式所示，复合变换的先后顺序是从第一个与点/向量相乘的矩阵开始的：

\[ \mathbf{A}_n\cdots\mathbf{A}_2\mathbf{A}_1\cdot\begin{bmatrix}x\\y\\1\end{bmatrix}= \mathbf{A}_n(\cdots(\mathbf{A}_2(\mathbf{A}_1\cdot\boldsymbol{v}))) \]

由于矩阵乘法符合结合律，可用只用一个矩阵 \(\mathbf M=\mathbf{A}_n\cdots\mathbf{A}_2\mathbf{A}_1\) 来表示一系列的变换操作：

\[ \mathbf{A}_n\cdots\mathbf{A}_2\mathbf{A}_1\cdot\begin{bmatrix}x\\y\\1\end{bmatrix}=\mathbf M\cdot\begin{bmatrix}x\\y\\1\end{bmatrix} \]

2.3 分解复合变换

如上图所示，需要将一个图形一个固定点旋转时，直接使用旋转变换是不起作用的（旋转变换以原点位中心）。

因此可以把这个变换分解为：

• 将旋转中心移动至圆心（当然图像也要一起移动）
• 绕圆心旋转对应角度
• 重新将旋转中心移动至原处

其复合变换 \(\mathbf M = \mathbf T(c)\cdot\mathbf R(\alpha)\cdot\mathbf T(-c)\)

3 3D 变换

与 2D 变换的齐次坐标矩阵类似，3D 变换矩阵定义如下：

• 点表示为 \((x,y,z,1)^T\)

• 矢量表示为 \((x,y,z,0)^T\)

• \((x,y,z,w)^T\) 表示点 \((x/w,y/w,z/w,1)^T \;(w\neq0)\)

• 缩放矩阵：

  \[ \mathbf S(s_x,s_y,s_z)= \begin{bmatrix} s_x&0&0&0\\ 0&s_y&0&0\\ 0&0&s_z&0\\ 0&0&0&1 \end{bmatrix} \]

• 平移矩阵：

  \[ \mathbf T(t_x,t_y,t_z)= \begin{bmatrix} 1&0&0&t_x\\ 0&1&0&t_y\\ 0&0&1&t_z\\ 0&0&0&1 \end{bmatrix} \]

旋转矩阵在 3D 变换中比较特殊，分为三种旋转：

• 绕 \(X\) 轴旋转

  \[ \mathbf R_x(\alpha)= \begin{bmatrix} 1&0&0&0\\ 0&\cos\alpha&-\sin\alpha&0\\ 0&\sin\alpha&\cos\alpha&0\\ 0&0&0&1 \end{bmatrix} \]

• 绕 \(Y\) 轴旋转

  xy = z

  yz = x

  zx = -xz = y

  \[ \mathbf R_y(\alpha)= \begin{bmatrix} \cos\alpha&0&\sin\alpha&0\\ 0&1&0&0\\ -\sin\alpha&0&\cos\alpha&0\\ 0&0&0&1 \end{bmatrix} \]

• 绕 \(Z\) 轴旋转

  \[ \mathbf R_x(\alpha)= \begin{bmatrix} \cos\alpha&-\sin\alpha&0&0\\ \sin\alpha&\cos\alpha&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{bmatrix} \]

将三种旋转复合，被称作欧拉角：

\[ \mathbf R_{xyz}(\alpha,\beta,\gamma)=\mathbf R_x(\alpha)\mathbf R_y(\beta)\mathbf R_z(\gamma) \]

以前后方向的轴旋转叫做 Roll

以左右方向的轴旋转叫做 Pitch

以上下方向的轴旋转叫做 Yaw

3.1 罗德里格旋转公式

罗德里格旋转公式（Rodrigues’ rotation formula），是计算三维空间中，一个向量绕任意过原点旋转轴旋转后得到的新向量的计算公式。 \[ \mathbf R(\boldsymbol n,\alpha)=\cos(\alpha)\mathbf I+ (1-\cos\alpha)\boldsymbol{nn^{\mathbf T}}+ \sin\alpha \underbrace{ \begin{bmatrix} 0&-n_z&n_y\\ n_z&0&-n_x\\ -n_y&n_x&0 \end{bmatrix} }_{\mathbf N} \]

\(\mathbf N\) 矩阵是向量 \(\boldsymbol n\) 的叉乘矩阵

4 视图变换（View/Camera Transformation）

先定义相机：

• 位置：\(\boldsymbol e\)

• 面朝向：\(\hat{\boldsymbol g}\)

• 向上方向：\(\hat{\boldsymbol t}\)

为了方便计算，约定相机在原点，面朝 \(-Z\) ，上朝 \(Y\)，同时对相机拍摄的物体应用相机的移动（即物体跟随相机移动）

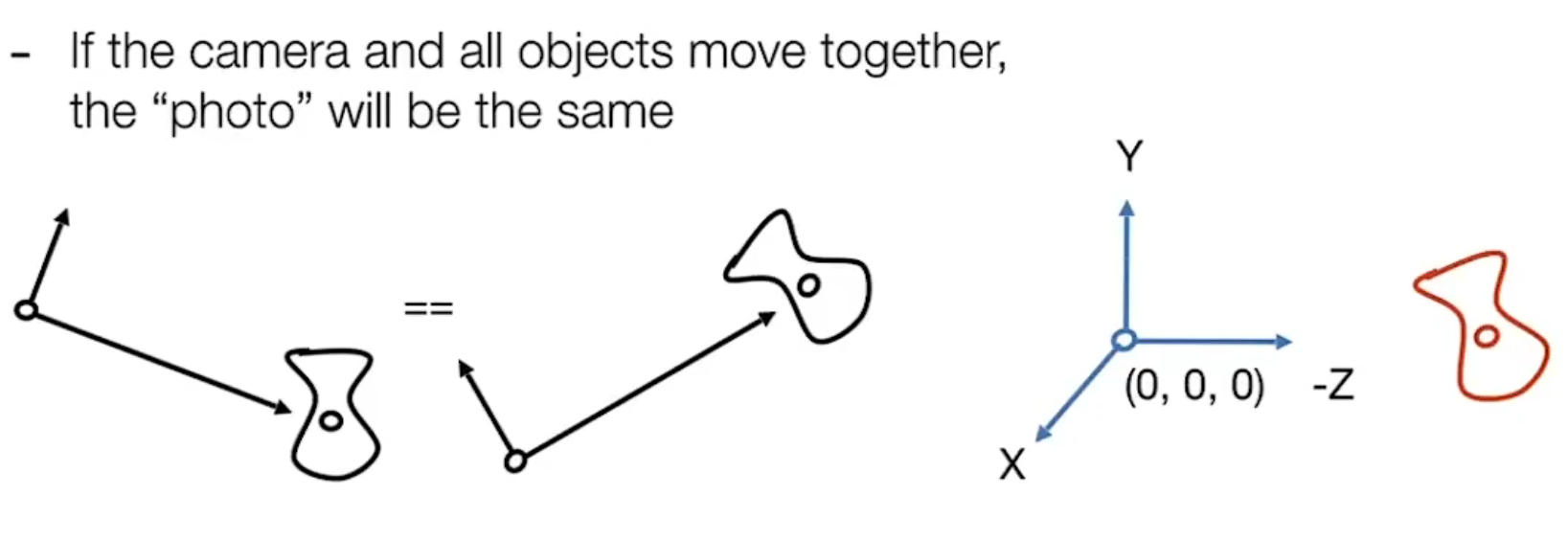
相机的变换矩阵定义为：

\[ \mathbf M_{view}=\mathbf R_{view}\mathbf T_{view} \]

\[ \mathbf T_{view}= \begin{bmatrix} 1&0&0&-x_e\\ 0&1&0&-y_e\\ 0&0&1&-z_e\\ 0&0&0&1 \end{bmatrix} \]

由于直接求相机转到约定朝向的旋转矩阵不好求，为此利用旋转矩阵是正交矩阵的特点，先求从约定朝向转到当前朝向的旋转矩阵。

\[ \mathbf R^{-1}_{view}= \begin{bmatrix} x_{\hat g\times\hat t}&x_{\hat t}&x_{-g}&0\\ y_{\hat g\times\hat t}&y_{\hat t}&y_{-g}&0\\ z_{\hat g\times\hat t}&z_{\hat t}&z_{-g}&0\\ 0&0&0&1 \end{bmatrix} \]

然后将其转置就可以得到我们需要的旋转矩阵了。

\[ \mathbf R_{view}= \begin{bmatrix} x_{\hat g\times\hat t}&y_{\hat g\times\hat t}&z_{\hat g\times\hat t}&0\\ x_{\hat t}&y_{\hat t}&z_{\hat t}&0\\ x_{-g}&y_{-g}&z_{-g}&0\\ 0&0&0&1 \end{bmatrix} \]

5 投影变换（Projection Transformation）

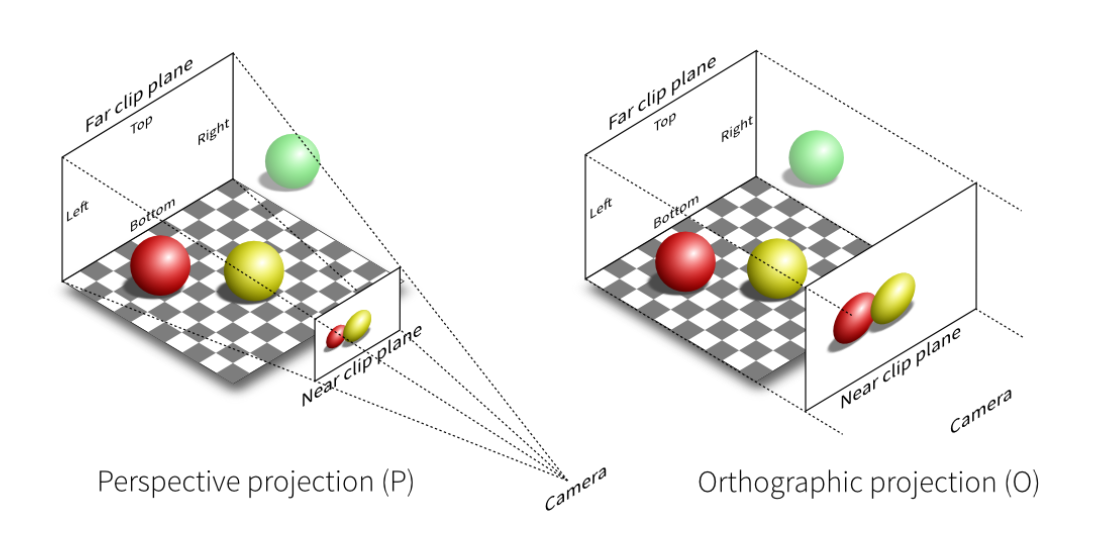
投影变换的目的是将 3D 投影为 2D 画面，主要分为

• 正交投影（orthographic projection）：两个平行边保持平行。
• 透视投影（perspective projection）：两个平行延长后会相交在一个点。会有近大远小的效果

为什么要有远平面？定义远平面是为了让在远平面外的物体直接被裁剪掉，节约运算资源

5.1 正交投影变换

将上图的正交投影定义为一个长方体，\([l,r]\times[b,t]\times[f,n]\)，然后将其映射到一个正则化的正方体上，\([-1,1]^3\)。

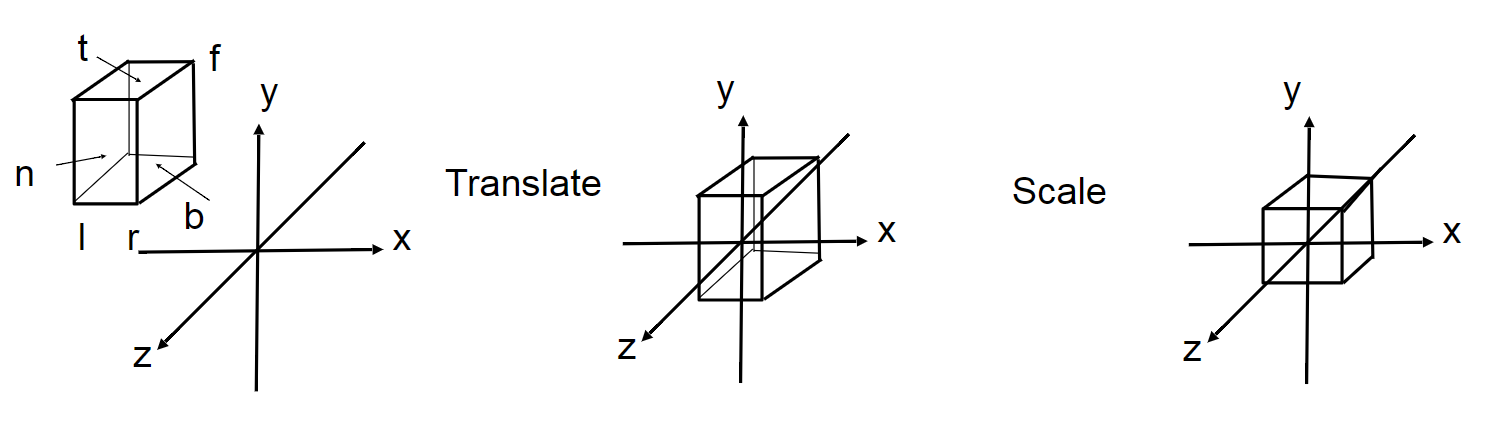
具体步骤：

• 将长方体的中心平移到原点
• 将长方体缩放到长宽高为 2 的正方体

变换矩阵（没有考虑旋转）如下：

\[ \mathbf M_{ortho}= \begin{bmatrix} \frac{2}{r-l}&0&0&0\\ 0&\frac{2}{t-b}&0&0\\ 0&0&\frac{2}{n-f}&0\\ 0&0&0&1 \end{bmatrix} \begin{bmatrix} 1&0&0&-\frac{l+r}{2}\\ 0&1&0&-\frac{b+t}{2}\\ 0&0&1&-\frac{n+f}{2}\\ 0&0&0&1 \end{bmatrix}= \begin{bmatrix} \frac{2}{r-l}&0&0&\frac{l+r}{l-r}\\ 0&\frac{2}{t-b}&0&\frac{b+t}{b-t}\\ 0&0&\frac{2}{n-f}&\frac{f+n}{f-n}\\ 0&0&0&1 \end{bmatrix} \]

由于约定是看向 -Z ，所以 n > f

5.2 透视投影变换

将截锥体挤到以近平面（投影平面）为基准的长方体（当然这个变换要应用到截锥体空间内的所有物体），然后进行正交投影。这样就完成了透视投影。

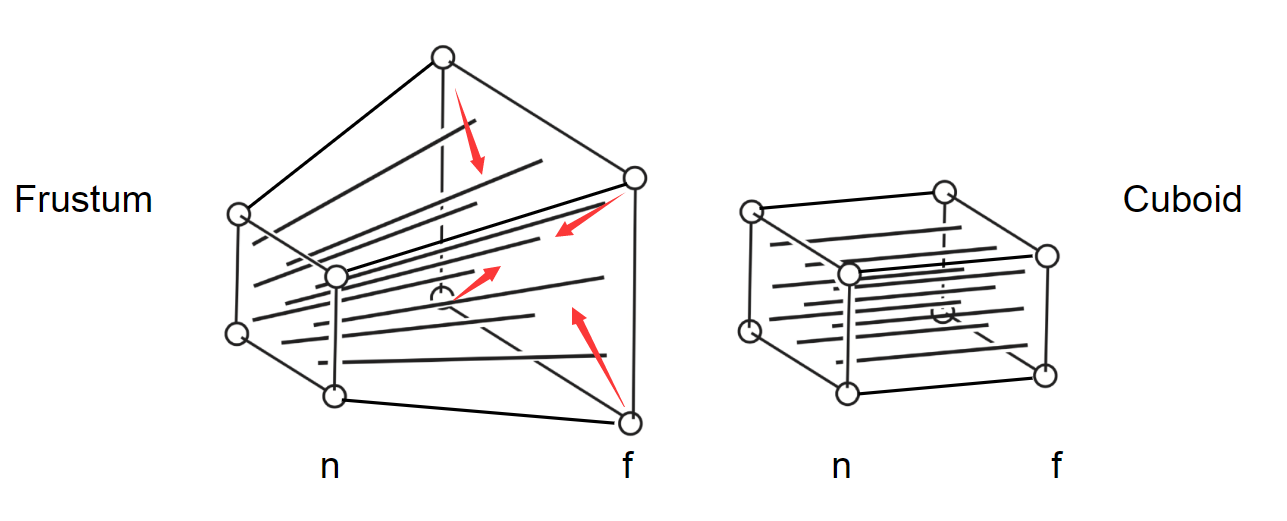
这样挤压有三个特点：

• 近平面所有点的位置不变
• 远平面所有点在 Z 轴的值不变
• 远平面中点的位置不变

从侧面看，对于任意点的位置变化，可以通过相似三角形的性质得到：

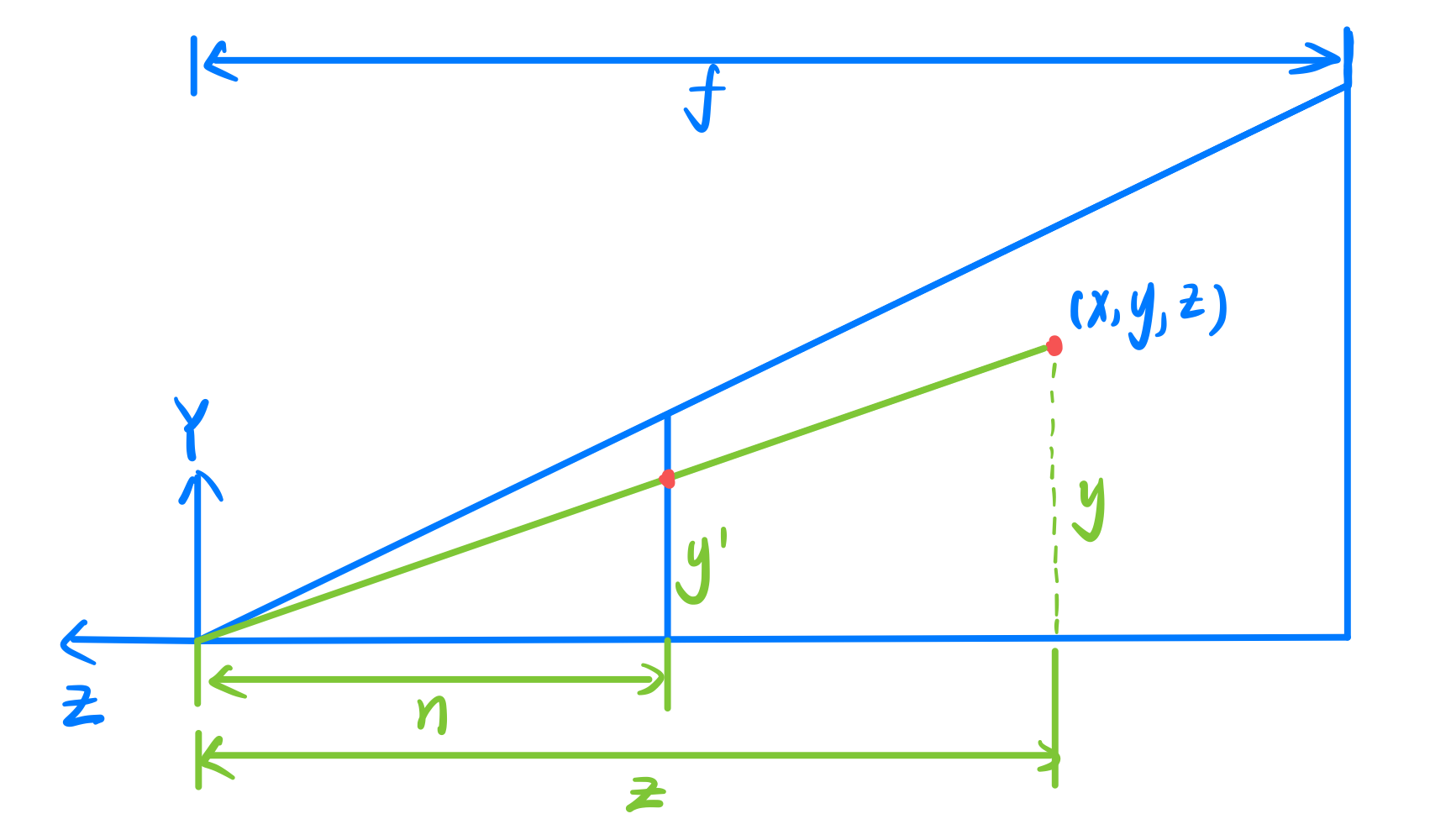\[ y'=\frac{n}{z}y \] 同理 \[ x'=\frac{n}{z}x \]

由于没有任何矩阵能实现 \[ \begin{bmatrix} x\\y\\z\\1 \end{bmatrix} \Rightarrow \begin{bmatrix} \frac{nx}{z}\\\frac{ny}{z}\\?\\1 \end{bmatrix} \] 在此可以利用齐次坐标下的特性

这样问题就变成： \[ \mathbf M_{persp\to ortho}^{(4\times 4)} \begin{bmatrix} x\\y\\z\\1 \end{bmatrix} = \begin{bmatrix} nx\\ny\\?\\z \end{bmatrix} \]

\[ \begin{bmatrix} n&0&0&0\\ 0&n&0&0\\ ?&?&?&?\\ 0&0&1&0 \end{bmatrix} \begin{bmatrix} x\\y\\z\\1 \end{bmatrix} = \begin{bmatrix} nx\\ny\\?\\z \end{bmatrix} \]

带入近平面上的点（即 z = n）可知： \[ \begin{bmatrix} n&0&0&0\\ 0&n&0&0\\ ?&?&?&?\\ 0&0&1&0 \end{bmatrix} \begin{bmatrix} x\\y\\n\\1 \end{bmatrix} = \begin{bmatrix} nx\\ny\\n^2\\n \end{bmatrix} \] 所以第三行的计算与 x, y 无关，得到 \[ \mathbf M_{persp\to ortho}= \begin{bmatrix} n&0&0&0\\ 0&n&0&0\\ 0&0&A&B\\ 0&0&1&0 \end{bmatrix} \] 为了算出 A，B 的值，带入远平面上的点可以得到二元一次方程 \[ \begin{align} An+B=n^2 \\ Af+B=f^2 \end{align} \] 解得 \[ \mathbf M_{persp\to ortho}= \begin{bmatrix} n&0&0&0\\ 0&n&0&0\\ 0&0&n+f&-nf\\ 0&0&1&0 \end{bmatrix} \] 最后透视投影矩阵可以表示为 \[ \mathbf M_{persp}=\mathbf M_{ortho}\mathbf M_{persp\to ortho} \]

需要注意的是，经过透视变换后，物体的 z 坐标和变换前的已经不是线性关系了。 \[ z_{out} = n + f - \frac{nf}{z_{in}} \] 为了方便观察，对 \(n, f\) 取正。可以得到下图：

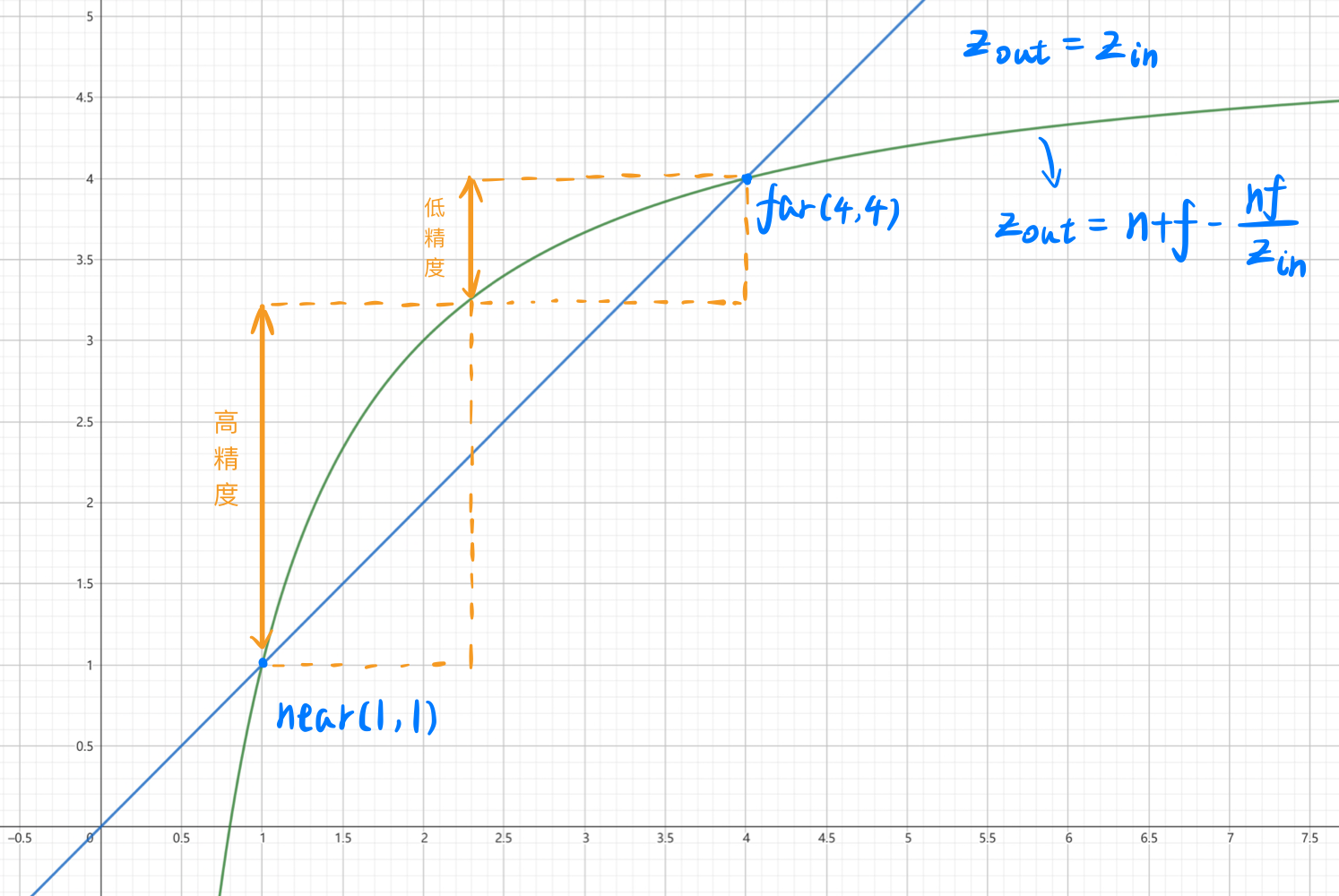
可以看出，经过透视投影后，物体 z 坐标变大了，即远离摄像头的位置（\(z_{out}>z_{in}\)）。

此外，我们还可以发现，靠近近平面的 z 坐标精度比靠近远平面的更高（z 能够表示的范围更大）。这一个特点可以解决近处明显的 z-fighting 问题。

z-fighting 是指两个三角形距离过于靠近，而浮点型的精度不够，最后无法准确判断两者前后关系，导致图像闪烁的问题。

详细信息可见：<渲染基础>-3D渲染中的Z-fighting现象

此外，我们可以注意到经过透视投影变换后，点的向量已经变为 \((nx,ny,z_{out},z_{in})\) 。此时 \(w\) 中存储的值正式原始的深度坐标，对于后续需要用到原始深度坐标的计算，我们直接使用 \(w\) 即可。

5.3 视角（FOV）和纵横比（aspect ratio）

在投影变换中，我们通过 \([l,r]\times[b,t]\) 定义了投影平面，但是实际生产中，人们使用的最多的参数是：

• 视角（field of view，FOV）：视角分为垂直视角和水平视角（游戏中水平视角用的比较多）。
• 纵横比（aspect ratio)：即我们实际所看到的画面的比例，如 1920 : 1080、1200 : 720等。

通过视角和纵横比我们就可以计算出 l，r，b，t。

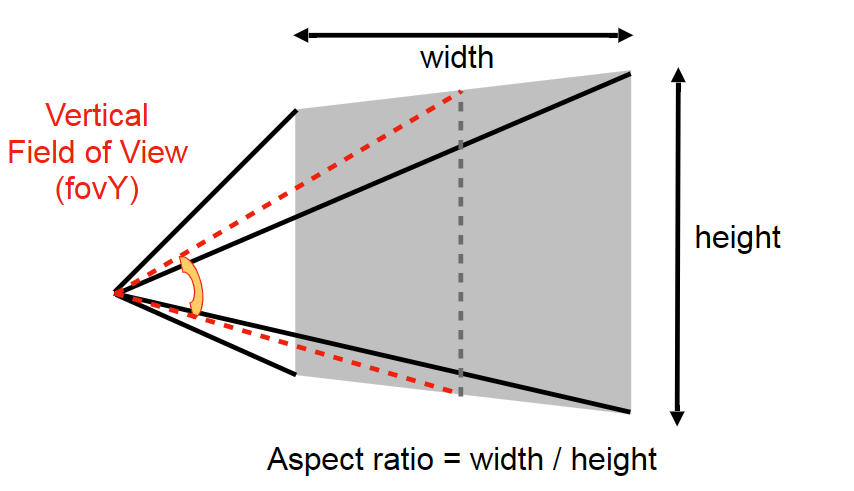
这里用的是垂直视角，水平视角和垂直视角可以藉由纵横比相互转换

设相机位于原点，上朝 Y 轴正方向，面朝 Z 轴负方向。利用三角函数和边的关系可以得到： \[ t=|n|\cdot\tan{\frac{fovY}{2}} \]

\[ r=aspect\cdot t \]

\[ b = -t\ \ \ l = -r \]