层序遍历找最右结点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 vector<int > rightSideView (TreeNode* root) int > res;if (root) que.push (root); while (!que.empty ())int size = que.size ();int last = 0 ;while (size--)front ();if (cur->left) que.push (cur->left);if (cur->right) que.push (cur->right);pop ();push_back (last);return res;
每层先访问右节点,记录每层遇到的第一个节点即为最右结点。
1 2 3 4 5 6 7 8 9 void dfs (TreeNode* cur, vector<int >& res, int depth) if (!cur) return ;if (res.size () == depth) res.emplace_back (cur->val);dfs (cur->right, res, depth + 1 );dfs (cur->left, res, depth + 1 );
637. 二叉树的层平均值(Easy)
513. 找树左下角的值(Medium)
1 2 3 4 5 6 7 8 9 10 11 12 void dfs (vector<int >& res, TreeNode* cur, int depth) if (!cur) return ;if (res.size () == depth)emplace_back (cur->val);else max (cur->val, res[depth]);dfs (res, cur->left, depth + 1 );dfs (res, cur->right, depth + 1 );
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 vector<int > bfs (TreeNode* root) int > res;if (root) que.push (root);while (!que.empty ())int size = que.size ();int m = INT_MIN;while (size--)front ();pop ();if (cur->val > m) m = cur->val;if (cur->left) que.push (cur->left);if (cur->right) que.push (cur->right);push_back (m);return res;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void dfs (TreeNode* cur, int & res, int depth) if (!cur) return ;max (res, depth)dfs (cur->left, res, depth + 1 );dfs (cur->right, res, depth + 1 );int maxDepth (TreeNode* root) int res = 0 ;dfs (root, res, 1 );return res;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 int bfs (TreeNode* root) int res = 0 ;if (root) que.push (root);while (!que.empty ())int size = que.size ();while (size--)front ();pop ();if (cur->left) que.push (cur->left);if (cur->right) que.push (cur->right);return res;
最小深度即为第一次遇到节点左右孩子都为空。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void dfs (TreeNode* cur, int & res, int depth) if (!cur)min (depth, res);return ;if (!cur->left && !cur->right)min (depth, res);dfs (cur->left, res, depth + 1 );dfs (cur->right, res, depth + 1 );
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 int bfs (TreeNode* root) int res = 0 ;if (root) que.push (root);while (!que.empty ())int size = que.size ();while (size--)front ();pop ();if (!cur->left && !cur->right)return res;if (cur->left) que.push (cur->left);if (cur->right) que.push (cur->right);return res;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Node* connect (Node* root) if (root) que.push (root);while (!que.empty ())int size = que.size ();for (int i = 0 ; i < size; i++)front ();pop ();if (i < size - 1 )front ();if (cur->left) que.push (cur->left);if (cur->right) que.push (cur->right);return root;
因为需要额外的队列空间来维护结点,所以空间复杂度为
每层都提前将下层的结点向右连接起来,之后到下一层只需通过 next 遍历,不需要额外的队列空间。空间复杂度
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Node* connect (Node* root) if (!root) return nullptr ;while (level)while (cur)if (cur->next)return root;
这道题是 116 的进阶版,树不再是 完美/满二叉树 。对于广度优先来说和 116 没有任何区别,不过想要做到空间复杂度为
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 Node* connect (Node* root) if (!root) return nullptr ;while (level)nullptr ;while (cur)if (cur->left)if (pre) pre->next = cur->left;if (cur->right)if (pre) pre->next = cur->right;while (level)if (level->left)break ;if (level->right)break ;return root;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 Node* connect (Node* root) if (!root) return nullptr ;new Node (0 );while (cur)nullptr ;while (cur)if (cur->left)if (cur->right)return root;
一颗平衡二叉树其每个节点的左右子树高度差不超过 1。所以我们需要对输入的二叉树每个节点的左右子树高度进行计算。
需要先计算当前结点的高度就需要先知道左右子树的高度,所以需要使用后序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 int treeHeight (TreeNode* cur) if (!cur) return 0 ;int hL = treeHeight (cur->left);int hR = treeHeight (cur->right);if (hL == -1 || hR == -1 ) return -1 ; if (abs (hL - hR) > 1 ) return -1 ;return max (hL, hR) + 1 ;bool isBalanced (TreeNode* root) return treeHeight (root) != -1 ;
计算深度的时候不会出现 0 - (-1) 或 -1 - 0 的情况,所以可以不用判断左右最大深度返回值是否为 -1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 int treeDepth (TreeNode* cur, int depth) if (!cur) return depth - 1 ;int dL = treeDepth (cur->left, depth + 1 );int dR = treeDepth (cur->right, depth + 1 );if (abs (dL - dR) > 1 ) return -1 ;return max (dL, dR);bool isBalanced (TreeNode* root) return treeDepth (root, 1 ) != -1 ;
该题需要输出二叉树的路径,所以我们除去存储每个路径的数组外,还需要一个 string 变量来存储路径的值。
在本题中,-> 是一个较为麻烦的处理点。如果每个结点之后跟随一个 -> 则需要再最后一个结点添加判断,或者在根结点分开,如下所示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void path (TreeNode* cur, vector<string>& res, string p) if (!cur) return ;"->" + to_string (cur->val);if (!cur->left && !cur->right) res.emplace_back (p);path (cur->left, res, p);path (cur->right, res, p);vector<string> binaryTreePaths (TreeNode* root) if (!root->left && !root->right) return {{to_string (root->val)}};path (root->left, res, to_string (root->val));path (root->right, res, to_string (root->val));return res;
但是还有一个更简介的办法,就是利用回溯的特点,如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 void path (TreeNode* cur, vector<string>& res, string p) if (!cur) return ;to_string (cur->val);if (!cur->left && !cur->right)emplace_back (p);return ;path (cur->left, res, p + "->" );path (cur->right, res, p + "->" );vector<string> binaryTreePaths (TreeNode* root) path (root, res, "" );return res;
该题需要找到一棵二叉树中所有路径和为 targetSum 的路径,并输出。因此我们需要在遍历一棵树的同时,记录路径和和结点的值。为了正确获得路径顺序,应该使用前序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 vector<vector<int >> res;int > tmpPath;void path (TreeNode* cur, int target) if (!cur) return ;emplace_back (cur->val);if (target == cur->val && !cur->left && !cur->right)emplace_back (tmpPath);path (cur->left, target - cur->val); path (cur->right, target - cur->val); pop_back (); int >> pathSum (TreeNode* root, int targetSum)path (root, targetSum);return res;
112. 路径总和(Easy)
利用递归不难写出:
1 2 3 4 5 6 7 8 9 10 11 TreeNode* searchBST (TreeNode* cur, int val) if (!cur) return nullptr ;if (val == cur->val) return cur;if (val <= cur->val)return searchBST (cur->left, val);else return searchBST (cur->right, val);
由于 BST 本身的有序性,不需要回溯,可以不使用栈或者队列进行迭代
1 2 3 4 5 6 7 8 9 10 11 12 13 14 TreeNode* searchBST (TreeNode* cur, int val) while (cur)if (val < cur->val)else if (val > cur->val)else return cur;return nullptr ;
一颗 BST 树经过中序遍历后是从小到大递增的。
递归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 TreeNode* pre == nullptr ;bool isValidBST (TreeNode* cur) if (!cur) return true ;bool left = isValidBST (cur->left);if (!pre || cur->val > pre->val)else return false ;bool right = isValidBST (cur->right);return left && right;
迭代
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 bool isValidBST (TreeNode* root) int64_t preVal = LLONG_MIN; while (cur || !stk.empty ())if (cur)push (cur);else top (); stk.pop ();if (cur->val > preVal)else return false ;return true ;
530. 二叉搜索树的最小绝对差(Easy)
每个结点左子树上所有值均小于这个结点的值,所以可以确定左子树的上限 maxVal 。
每个结点右子树上所有值均大于这个结点的值,所以可以确定左子树的下限 minVal 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 bool check (TreeNode* cur, int64_t minVal, int64_t maxVal) if (!cur) return true ;if (cur->val >= maxVal || cur->val <= minVal)return false ;return check (cur->left, minVal, cur->val) && check (cur->right, cur->val, maxVal);bool isValidBST (TreeNode* root) return check (root, LLONG_MIN, LLONG_MAX);
对于非二插搜索树的情况,通常用哈希表统计不同值的数量,需要额外的空间。而二叉搜索树的中序遍历是有序递增的,所以可以直接中序遍历二叉树,然后统计最大数量的值。
此外该题可能出现复数个众数,所以需要在发现新众数时清空所有旧的众数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 int preVal, cnt, maxCnt;void traversal (TreeNode* cur, vector<int >& res) if (!cur) return ;traversal (cur->left, res); if (preVal == cur->val)else 1 ;if (cnt == maxCnt) emplace_back (cur->val);if (cnt > maxCnt) int > {cur->val}; traversal (cur->right, res); vector<int > findMode (TreeNode* root) int > res;traversal (root, res);return res;
根据二叉搜索树的特性,我们可以知道 p, q 与公共祖先的位置关系:
p,q 都小于该节点:则说明最近公共祖先一定在当前结点左边
p,q 都大于该节点:则说明最近公共祖先一定在当前结点右边
除去以上情况,就只剩下两种情况
p, q 分别在当前结点左右
p, q 中有一个是当前结点
这就说明该结点就是最小公共祖先
递归
1 2 3 4 5 6 7 8 9 10 11 TreeNode* lowestCommonAncestor (TreeNode* cur, int p, int q) if (!cur) return cur;if (p < cur->val && q < cur->val)return lowestCommonAncestor (cur->left, p, q);if (p > cur->val && q > cur->val)return lowestCommonAncestor (cur->right, p, q);return cur;
迭代
1 2 3 4 5 6 7 8 9 10 11 12 13 14 TreeNode* lowestCommonAncestor (TreeNode* cur, TreeNode* p, TreeNode* q) while (cur)if (p->val < cur->val && q->val < cur->val)else if (p->val > cur->val && q->val > cur->val)else break ;return cur;
不考虑平衡,直接利用 BST 的性质快速找到插入的位置2
1 2 3 4 5 6 7 8 9 10 11 TreeNode* insertIntoBST (TreeNode* cur, int val) if (!cur) return new TreeNode (val);if (val < cur->val)insertIntoBST (cur->left, val);if (val > cur->val)insertIntoBST (cur->right, val);return cur;
要删除 BST 中的节点还要保证删除后的树仍为 BST,需要考虑以下五种情况:
找不到删除结点
待删除结点为叶子
待删除结点存在左子树
待删除结点存在右子树
待删除结点同时存在左右子树
找到右子树的最左结点,让左子树作为其左子树
返回右子树
实际上上述五种情况还可以简化,情况 2 实际上通过 3, 4 就可以实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 TreeNode* deleteNode (TreeNode* cur, int key) if (!cur) return nullptr ;if (key < cur->val)deleteNode (cur->left, key);else if (key > cur->val)deleteNode (cur->right, key);else if (!cur->left) return cur->right;if (!cur->right) return cur->left;while (tmp->left)return cur->right;return cur;
因为树是LeetCode创建的,遵循谁分配的谁释放原则,不 delete 结点。否则提交到 LeetCode 会出现释放后被使用的问题
https://zhuanlan.zhihu.com/p/547202945
此题要求裁剪掉二叉树中超出范围的结点,所以一个基本的逻辑就是遇到超出范围的结点就直接返回 null 。
但是对于删除的结点,其右子树的结点中可能存在大于 low 的结点,或者左子树存在小于 high 的结点。所以我们还要对其子树进行修剪,然后返回符合条件的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 TreeNode* trimBST (TreeNode* cur, int low, int high) if (!cur) return nullptr ;if (cur->val < low)return trimBST (cur->right, low, high); if (cur->val > high)return trimBST (cur->left, low, high); trimBST (cur->left, low, high);trimBST (cur->right, low, high);return cur;
因为数组是有序的,所以不断的找到中间的分割点,然后将左和右的数作为其子树,重复这个过程就可以构建出一个平衡的 BST 。
为了节约时间空间成本,使用左右下标 bg,ed 来分割数组。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 TreeNode* makeBST (vector<int >& nums, int bg, int ed) if (bg >= ed) return nullptr ;int mid = ed + ((bg - ed) >> 1 );auto cur = new TreeNode (nums[mid]);makeBST (nums, bg, mid);makeBST (nums, mid + 1 , ed);return cur;TreeNode* sortedArrayToBST (vector<int >& nums) return makeBST (nums, 0 , nums.size ());
这道题实际上是从大到小顺序,每个值加上前一个值作为其更新值。所以使用 右中左 序遍历即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int preSum = 0 ;TreeNode* convertBST (TreeNode* cur) if (!cur) return nullptr ;convertBST (cur->right);convertBST (cur->left);return cur;
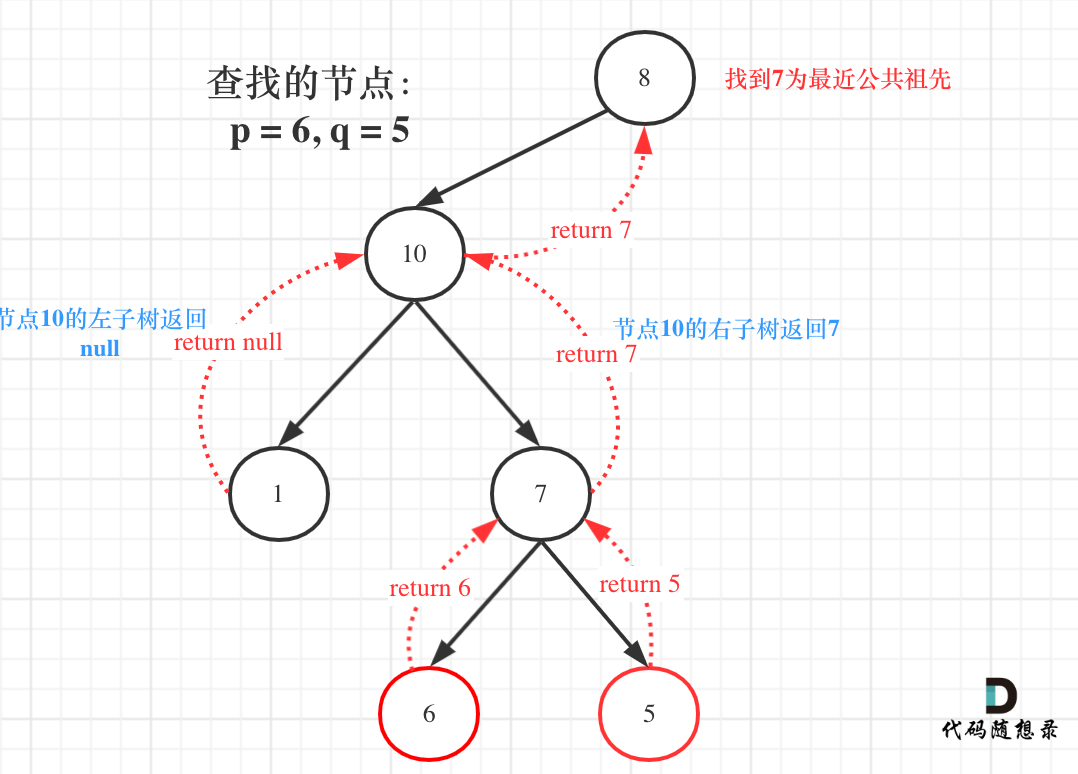
要找到二叉树的最近公共祖先,最好的办法是从下往上找,所以后序遍历是最符合需求的。
因为我们是从下往上找,所以当第一次遇到结点的左右分别找到 p, q 时,就说明该节点是最近公共祖先了。然后待解决的问题只有两个:
如何知道是否找到 p, q ?
遍历到 p 或者 q 就返回他们,如果一直没找到,则返回 null (遍历到了空节点)
如果左右返回值均不为空,则说明已经找到了最近公共祖先
如何将找到的最近公共祖先返回?
当我们找到公共祖先时,就返回该结点
这样,当 left 和 right 中只有一个为空时,就说明另一个就是我们找到的答案,继续向上层返回
1 2 3 4 5 6 7 8 9 10 11 12 13 14 TreeNode* lowestCommonAncestor (TreeNode* cur, TreeNode* p, TreeNode* q) if (!cur || cur == p || cur == q) return cur;lowestCommonAncestor (cur->left, p, q);lowestCommonAncestor (cur->right, p, q);if (left && right) return cur;if (!left && right) return right; return left;
从上往下找的话,我们需要不断地更新更节点,然后寻找其左右是否有 p, q,时间复杂度大大增大
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 bool findTarget (TreeNode* cur, TreeNode* t) if (!cur)return false ;if (cur == t)return true ;return findTarget (cur->left, t) || findTarget (cur->right, t);TreeNode* lowestCommonAncestor (TreeNode* cur, TreeNode* p, TreeNode* q) if (!cur) return nullptr ;bool pL = findTarget (cur->left, p) || cur == p;bool pR = findTarget (cur->right, p) || cur == p;bool qL = findTarget (cur->left, q) || cur == q;bool qR = findTarget (cur->right, q) || cur == q;if ((pL && qR) || (pR && qL)) return cur;if (pL)return lowestCommonAncestor (cur->left, p, q);return lowestCommonAncestor (cur->right, p, q);
100、101、572 这三道题是层层递进的关系。
判定条件变化后
运用于
100.相同的树
101.对称二叉树
572.另一棵树的子树
该题需要对传入的两颗树的每个节点比较是否相等。所以需要同时遍历两颗树。然后比较两颗树的左右子结点。
1 2 3 4 5 6 7 8 9 10 11 12 bool isSame (TreeNode* a, TreeNode* b) if (!a && !b) return true ;if (!a || !b) return false ;if (a->val != b->val) return false ;return isSame (a->left, b->left) && isSame (a->right, b->right);
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 bool isSameIteration (TreeNode* a, TreeNode* b) push (a);push (b);while (!que.empty ())front (); que.pop ();front (); que.pop ();if (!curA && !curB) continue ;if (!curA || !curB) return false ;if (curA->val != curB->val) return false ;push (curA->left);push (curB->left);push (curA->right);push (curB->right);return true ;
要判断一棵树是否轴对称,需要从外到内(内到外)判断两颗子树是否对称。即判断:
left->left 和 right->right
left->right 和 right->left
以下几种情况则说明不对称:
换句话说,满足以下条件则说明对称:
1 2 3 4 5 6 7 8 9 10 11 bool compare (TreeNode* left, TreeNode* right) if (!left && !right) return true ;if (!left || !right) return false ;bool outside = compare (left->left, right->right);bool inside = compare (left->right, right->left);return left->val == right->val && outside && inside;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 bool compareIteration (TreeNode* root) push (root->left);push (root->right);while (!que.empty ())front ();pop ();front ();pop ();if (!left && !right) continue ;if (!left || !right) return false ;if (left->val != right->val) return false ;push (left->left);push (right->right);push (left->right);push (right->left);return true ;
改题需要我们在一棵树中寻找是否存在与目标相同的子树。这与 100. 相同的树 的不同之处主要在于,进行比较的两棵树其中之一变为了一棵树的子树。
因此我们需要先确定子树的根节点,如果这课子树不满足,则需要找到下一颗子树进行比较。所以这个问题涉及到了两次递归(或多层迭代循环)。
子树是否相同判断
这里与 100. 相同的树 并无差异。
1 2 3 4 5 6 7 8 bool isSameTree (TreeNode* cur, TreeNode* subCur) if (!cur && !subCur) return true ;if (!cur || !subCur) return false ;if (cur->val != subCur->val) return false ;return isSameTree (cur->left, subCur->left) && isSameTree (cur->right, subCur->right);
遍历树种的子树
1 2 3 4 5 6 7 8 9 bool isSubtree (TreeNode* cur, TreeNode* subRoot) if (!cur) return false ;if (isSameTree (cur, subRoot)) return true ;return isSubtree (cur->left, subRoot) || isSubtree (cur->right, subRoot);
直接通过递归或者迭代遍历一棵树也可以得到其结点个数,其时间复杂度为
1 2 3 4 5 6 7 int countNodes (TreeNode* cur) if (!cur) return 0 ;return countNodes (cur->left) + countNodes (cur->right) + 1 ;
但是这道题的数是完全二叉树,我们可以利用其特性加快结点数量的计算。
一颗完全二叉树,除了最后一行的结点可以有空节点,其余每行都是填满的。这意味着,一颗完全二叉树的子树也是完全二叉树,而且有两种情况。
满二叉树 :这样可以通过树的高度直接通过公式 普通完全二叉树 :左右子树结点数之和。
判断一颗完全二叉树是否为满二叉树,可以利用以下性质:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 int count (TreeNode* cur) if (!cur) return 0 ;int cntL = 1 , cntR = 1 ;while (tmp)while (tmp)if (cntL == cntR) return (1 << cntL) - 1 ;return count (cur->left) + count (cur->right) + 1 ;
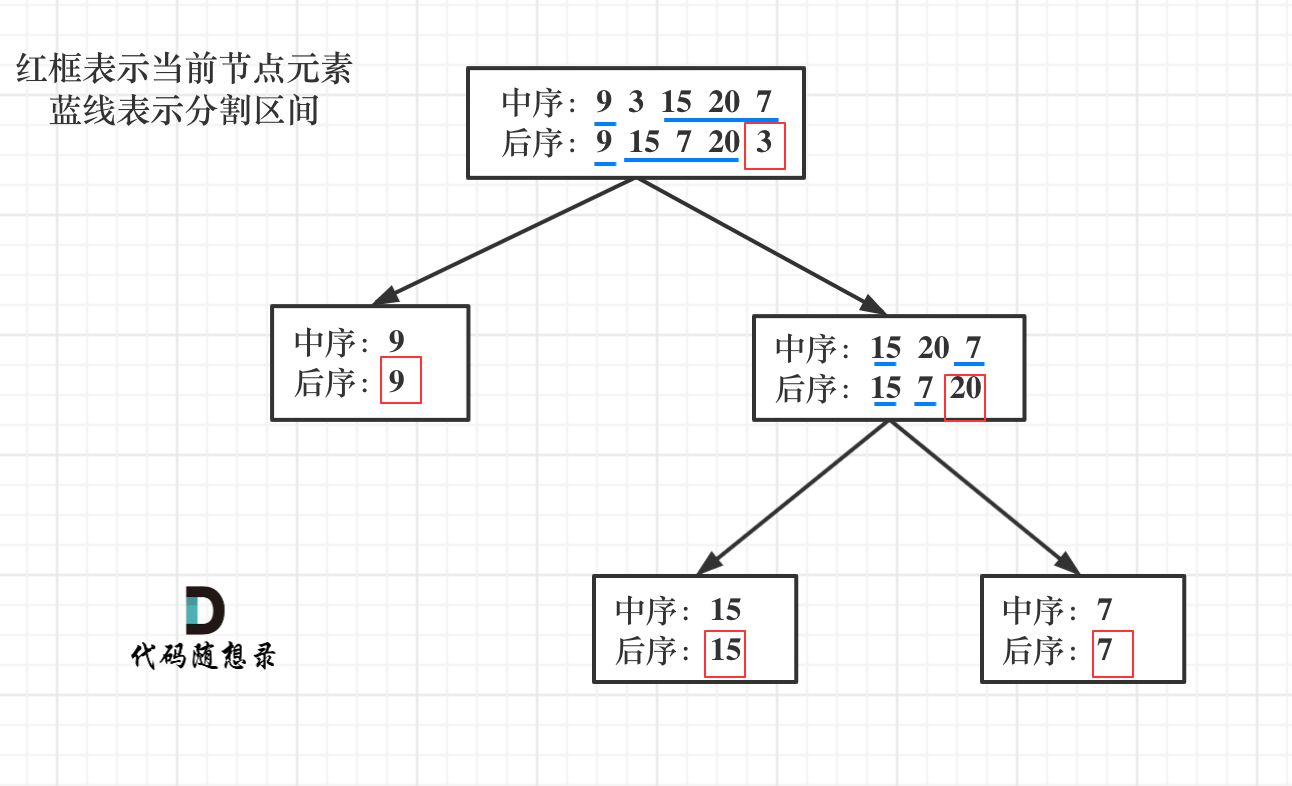
通过读取后序(左右中),我们可以知道中节点的值,之后在中序中找到它,就可以将两个数组序列切割成左右子树的中序和后序。
设中后序左右边界序号分别为 inL,inR,postL,postR 分割序号为 mid
首先很容易得到左右子树中序的边界
左子树:[inL, mid)
右子树:[mid + 1, inR)
对于后序左右子树的边界,可以利用后序与中序长度相等这一特点(需要注意是闭区间)
左子树:[postL, postL + mid - inL)
右子树:[postL + mid - inL, postR - 1)
此外为了不用每次通过循环找到分割节点的序号,可以使用哈希表提前存储中序的值与序号。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 unordered_map<int , int > inorderHash;int > post;TreeNode* dfs (int inL, int inR, int postL, int postR) if (postL == postR) return nullptr ;auto cur = new TreeNode (post[postR-1 ]);int mid = inorderHash[cur->val];dfs (inL, mid, postL, postL+mid-inL);dfs (mid+1 , inR, postL+mid-inL, postR-1 );return cur;TreeNode* buildTree (vector<int >& inorder, vector<int >& postorder) for (int i = 0 ; i < inorder.size (); i++)int size = inorder.size ();return dfs (0 , size, 0 , size);
该题和 106 类似,不过是前序 + 中序来建立树。所以不同之处主要在于边界的确定。
首先左右子树中序的边界还是没有变化
左子树:[inL, mid)
右子树:[mid + 1, inR)
不同之处在于前序的边界
左子树:[preL + 1, pre + 1 + mid - inL)
右子树:[pre + 1 + mid - inL, preR)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 unordered_map<int , int > inHash;int > pre;TreeNode* build (int preL, int preR, int inL, int inR) if (preL == preR) return nullptr ;auto cur = new TreeNode (pre[preL]);int mid = inHash[cur->val];build (preL+1 , preL+1 +mid-inL, inL, mid);build (preL+1 +mid-inL, preR, mid+1 , inR);return cur;TreeNode* buildTree (vector<int >& preorder, vector<int >& inorder) for (int i = 0 ; i < inorder.size (); i++)int size = preorder.size ();return build (0 , size, 0 , size);
通过左右边界限定范围,循环遍历出最大值的下标。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 TreeNode* build (const vector<int >& nums, int left, int right) if (left == right) return nullptr ;int maxValInd = left;for (int i = left; i < right; i++)if (nums[i] > nums[maxValInd])auto cur = new TreeNode (nums[maxValInd]);build (nums, left, maxValInd);build (nums, maxValInd + 1 , right);return cur;
遍历两颗树的同时,比较两棵树的结点,按照题目要求来就不难写出递归。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 TreeNode* mergeTrees (TreeNode* curA, TreeNode* curB) if (!curA && !curB) return nullptr ;if (!curA) return curB; if (!curB) return curA; mergeTrees (curA->left, curB->left);mergeTrees (curA->right, curB->right);return curA;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 TreeNode* mergeTrees (TreeNode* curA, TreeNode* curB) if (!curA && !curB) return nullptr ;if (!curA)new TreeNode (curB->val);mergeTrees (nullptr , curB->left);mergeTrees (nullptr , curB->right);else if (!curB)new TreeNode (curA->val);mergeTrees (curA->left, nullptr );mergeTrees (curA->right, nullptr );else new TreeNode (curA->val + curB->val);mergeTrees (curA->left, curB->left);mergeTrees (curA->right, curB->right);return cur;