回溯基础

回溯是一种暴力求解的方法，用于解决一些适合用递归的问题：

• 组合问题：N 个数里面按一定规则找出 k 个数的集合；
• 切割问题：一个字符串按一定规则有几种切割方式；
• 子集问题：一个 N 个数的集合里有多少符合条件的子集；
• 排列问题：N 个数按一定规则全排列，有几种排列方式；
• 棋盘问题：N皇后，解数独等；

所有问题的回溯解法都可以抽象为树形结构，树的宽度是集合的大小，递归的深度是树的高度（N 叉树）。

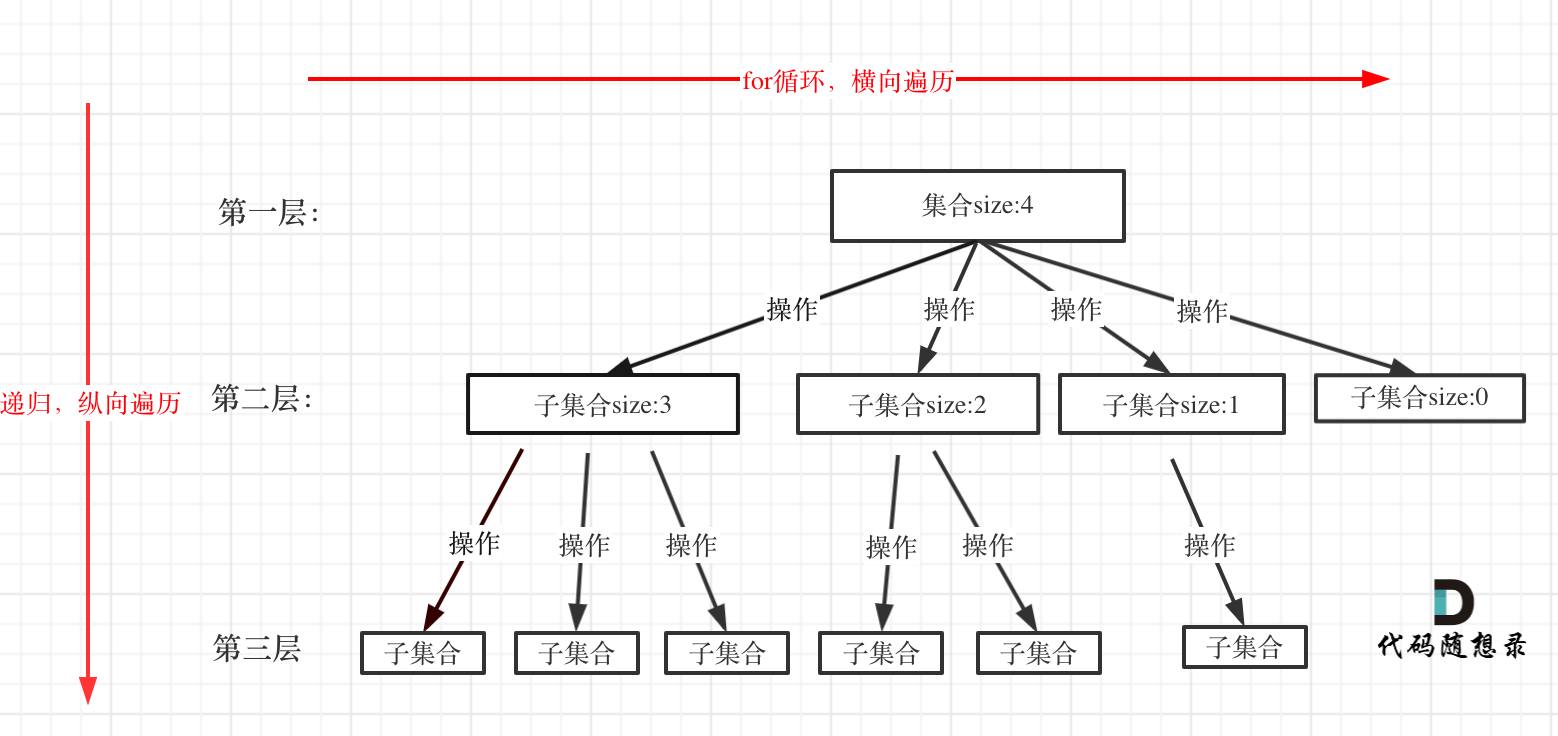
其模板为

void backtracking(参数) 
{
    if (终止条件) 
    {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) 
    {
        处理节点;
        backtracking(路径，选择列表);
        回溯，撤销处理结果
    }
}

为了提高回溯的效率，还可以进行剪枝操作，即对一些能够提前知晓没必要继续搜索的分支提前返回。